题目内容
 如图所示,质量为mA=4.9kg,长为L=0.5m,高为h=0.2m的木块A放在水平地面上,质量为mB=1kg的小木块B放在A的一端,质量为mC=0.1kg,初速度为v0=100m/s的子弹C从A的另一端射入并和它一起以共同速度运动(射入时间忽略不计).若A和B之间光滑,A和地面间摩擦因数为μ=0.25.求:
如图所示,质量为mA=4.9kg,长为L=0.5m,高为h=0.2m的木块A放在水平地面上,质量为mB=1kg的小木块B放在A的一端,质量为mC=0.1kg,初速度为v0=100m/s的子弹C从A的另一端射入并和它一起以共同速度运动(射入时间忽略不计).若A和B之间光滑,A和地面间摩擦因数为μ=0.25.求:(1)子弹射入A后到B第一次落地的时间t;
(2)A滑动的总距离S.
分析:(1)子弹射入A的过程,由于射入时间忽略不计,两者组成的系统动量守恒,可由动量守恒列式求出子弹射入A后,AC的共同速度.由于AB间光滑,所以B相对于地静止不动,当AC整体相对于地滑行距离L时B将落地,对AC整体,根据动能定理和动量定理列式求出B在A上滑行的时间,B离开A后做自由落体运动,根据自由落体运动的规律求出B下落的时间,即可求得总时间t.
(2)B离开A后,A作匀减速直线运动至速度为零,由动能定理求解此后A滑行的距离,即可得到总距离S.
(2)B离开A后,A作匀减速直线运动至速度为零,由动能定理求解此后A滑行的距离,即可得到总距离S.
解答:解:(1)C从A的一端射入并和它一起以速度v1运动的极短时间内,A、C组成的系统动量守恒,取向右为正方向,则有:
mCv0=(mA+mC)v1 …①
代入数据并解得:v1=
=
=2m/s… ②
因A和B之间光滑,B相对地处于静止,设B经时间t1离开A的瞬间,此时A的速度为v2,则由动能定理和动量定理得:
-f1L=
(mA+mB)
-
(mA+mC)
… ③
-f1t1=(mA+mB)
-(mA+mC)
…④
f1=μN=μ(mA+mB+mC)g…⑤
由以上各式联立求解得:t1=
s,v2=1m/s… ⑥
B离开A后作自由落体运动,则由 h=
g
得:t2=
=
=0.2s…⑦
子弹射入A后到B第一次落地的时间为:t=t1+t2=
+1=0.53s… ⑧
(2)B离开A后,A作匀减速直线运动至速度为零,则由动能定理得:
-f2S0=0-
(mA+mC)
… ⑨
f2=μN=μ(mA+mC)g… ⑩
由以上各式联立求解得:S0=
=
=0.2m…(11)
所以整个过程中A滑动的距离为:S=L+S0=0.7m…(12)
答:(1)子弹射入A后到B第一次落地的时间t为0.53s;
(2)A滑动的总距离S为0.7m.
mCv0=(mA+mC)v1 …①
代入数据并解得:v1=
| mCv0 |
| mA+mC |
| 0.1×100 |
| 4.9+0.1 |
因A和B之间光滑,B相对地处于静止,设B经时间t1离开A的瞬间,此时A的速度为v2,则由动能定理和动量定理得:
-f1L=
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| v | 2 1 |
-f1t1=(mA+mB)
| v | 2 |
| v | 1 |
f1=μN=μ(mA+mB+mC)g…⑤
由以上各式联立求解得:t1=
| 1 |
| 3 |
B离开A后作自由落体运动,则由 h=
| 1 |
| 2 |
| t | 2 2 |
|
|
子弹射入A后到B第一次落地的时间为:t=t1+t2=
| 1 |
| 3 |
(2)B离开A后,A作匀减速直线运动至速度为零,则由动能定理得:
-f2S0=0-
| 1 |
| 2 |
| v | 2 2 |
f2=μN=μ(mA+mC)g… ⑩
由以上各式联立求解得:S0=
| ||
| 2μg |
| 12 |
| 2×0.25×10 |
所以整个过程中A滑动的距离为:S=L+S0=0.7m…(12)
答:(1)子弹射入A后到B第一次落地的时间t为0.53s;
(2)A滑动的总距离S为0.7m.
点评:分析物理过程,把握每个过程遵守的物理规律是解决复杂物理问题的关键.本题分析时要注意AB间没有摩擦力,B先相对于地是不动的.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 如图所示,质量为mA=2kg的木板A静止在光滑水平面上,一质量为mB=1kg的小物块B以某一初速度vo从A的左端向右运动,当A向右运动的路程为L=0.5m时,B的速度为vB=8m/s,此时A的右端与固定竖直挡板相距x.已知木板A足够长(保证B始终不从A上掉下来),A与挡板碰撞无机械能损失,A、B之间的动摩擦因数为μ=0.2,g取10m/s2
如图所示,质量为mA=2kg的木板A静止在光滑水平面上,一质量为mB=1kg的小物块B以某一初速度vo从A的左端向右运动,当A向右运动的路程为L=0.5m时,B的速度为vB=8m/s,此时A的右端与固定竖直挡板相距x.已知木板A足够长(保证B始终不从A上掉下来),A与挡板碰撞无机械能损失,A、B之间的动摩擦因数为μ=0.2,g取10m/s2 (2013?许昌三模)如图所示,质量为mA=2kg的木块A静止在光滑水平面上.一质量为mB=1kg的木块B以某一初速度v0=5m/s沿水平方向向右运动,与A碰撞后都向右运动.木块A与挡板碰撞后立即反弹(设木块A与挡板碰撞过程无机械能损失).后来木块A与B发生二次碰撞,碰后A、B同向运动,速度大小分别为0.9m/s、1.2m/s.求:
(2013?许昌三模)如图所示,质量为mA=2kg的木块A静止在光滑水平面上.一质量为mB=1kg的木块B以某一初速度v0=5m/s沿水平方向向右运动,与A碰撞后都向右运动.木块A与挡板碰撞后立即反弹(设木块A与挡板碰撞过程无机械能损失).后来木块A与B发生二次碰撞,碰后A、B同向运动,速度大小分别为0.9m/s、1.2m/s.求:
 如图所示,质量为mA的物块A用不可伸长的细线吊着,在A的下方用弹簧连着质量为mB的物块B,开始时静止不动.现在B上施加一个竖直向下的力F,缓慢拉动B使之向下运动一段距离后静止(弹簧始终在弹性限度内),希望撤去力F后,B向上运动并能顶起A,则力F的最小值是( )
如图所示,质量为mA的物块A用不可伸长的细线吊着,在A的下方用弹簧连着质量为mB的物块B,开始时静止不动.现在B上施加一个竖直向下的力F,缓慢拉动B使之向下运动一段距离后静止(弹簧始终在弹性限度内),希望撤去力F后,B向上运动并能顶起A,则力F的最小值是( )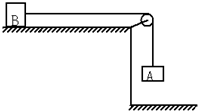 如图所示,质量为mA=1kg、mB=3kg的两个物体A和B.,用跨过定滑轮的细绳相连.用力把B压在水平桌面上.使A离地面的高度为H=2.0m,且桌面上方细绳与桌面平行.现撤去压B的外力.使A、B从静止开始运动,A着地后不反弹,在运动过程中B始终碰不到滑轮.B与水平桌面间的动摩擦因数为μ=0.2,不汁滑轮与轴间、绳子的摩擦、不计空气阻力及细绳和滑轮的质量,取g=10m/s2.求:
如图所示,质量为mA=1kg、mB=3kg的两个物体A和B.,用跨过定滑轮的细绳相连.用力把B压在水平桌面上.使A离地面的高度为H=2.0m,且桌面上方细绳与桌面平行.现撤去压B的外力.使A、B从静止开始运动,A着地后不反弹,在运动过程中B始终碰不到滑轮.B与水平桌面间的动摩擦因数为μ=0.2,不汁滑轮与轴间、绳子的摩擦、不计空气阻力及细绳和滑轮的质量,取g=10m/s2.求: