题目内容
如图所示,ABMNCD为某个游戏场中的竖直固定轨道示意图,水平直轨道MN与右边半径R=3m的3/4光滑圆弧轨道NCD底端相连接,水平直轨道左边通过光滑曲线轨道BN与高为h=1m的平台AB相连接,平台AB长为1两个可视为质点的小球,两球质量均为0.lkg,开始时两球紧靠在一起,若同时给a、b一个初动能,使a向左运动,b向右运动,a的初动能为Eka=2.2J,b的初动能为Ekb=3.0J,设a、b与水平轨道、与平台之间的动摩擦因数u均为0.2.为使a、b在以后的运动中不脱离平台与轨道,可适当调节轨道MN的长度、小球a、b运动的初始位置.求(1)符合要求的轨道MN的最短距离;
(2)在满足(1)条件下,a、b两球由于运动而损失的总机械能.
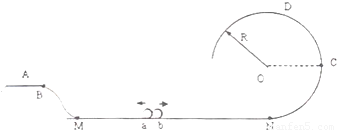
【答案】分析:(1)当a球向左运动时,恰好通过光滑曲线轨道BN到达平台AB的左边时,速度为零,动能转化为重力势能和摩擦生热,根据能量守恒定律列式,求出aM距离.
b向右运动时,为了运动中不脱离轨道,最大高度在 的圆周以下,然后返回,同样当其通过光滑曲线轨道BN到达平台AB的左边速度为零时,所需轨道最短,对b球,根据能量守恒列式,求出bN,即可得到MN最短距离;
的圆周以下,然后返回,同样当其通过光滑曲线轨道BN到达平台AB的左边速度为零时,所需轨道最短,对b球,根据能量守恒列式,求出bN,即可得到MN最短距离;
(2)初态时两球的总动能与末态时两球重力势能之差,即为损失的总机械能.
解答:解:(1)当a球向左运动时,假设开始运动时到M点的距离x1,则当其恰好通过光滑曲线轨道BN到达平台AB的左边时,速度为零,根据能量守恒定律得
mgh+μmg(x1+1)=Eka
得x1=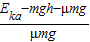 =
=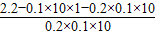 =5m
=5m
b向右运动时,假设开始运动时到N的距离为x2,为了运动中不脱离轨道,最大高度在 的圆周以下,然后返回,
的圆周以下,然后返回,
同样当其通过光滑曲线轨道BN到达平台AB的左边速度为零时,所需轨道最短.
对b球,根据能量守恒得
μmg(2x2+x1+1)+mgh=Ekb
解得,x2=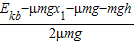 =2m
=2m
则MN=x1+x2=7m
(2)a、b两球由于运动而损失的总机械能为△E=Eka+Ekb-2mgh=3.2J
答:
(1)符合要求的轨道MN的最短距离是7m;
(2)在满足(1)条件下,a、b两球由于运动而损失的总机械能是3.2J.
点评:本题的关键是分析什么条件下才能保证a、b在运动中不脱离平台与轨道,根据能量守恒进行处理.
b向右运动时,为了运动中不脱离轨道,最大高度在
 的圆周以下,然后返回,同样当其通过光滑曲线轨道BN到达平台AB的左边速度为零时,所需轨道最短,对b球,根据能量守恒列式,求出bN,即可得到MN最短距离;
的圆周以下,然后返回,同样当其通过光滑曲线轨道BN到达平台AB的左边速度为零时,所需轨道最短,对b球,根据能量守恒列式,求出bN,即可得到MN最短距离;(2)初态时两球的总动能与末态时两球重力势能之差,即为损失的总机械能.
解答:解:(1)当a球向左运动时,假设开始运动时到M点的距离x1,则当其恰好通过光滑曲线轨道BN到达平台AB的左边时,速度为零,根据能量守恒定律得
mgh+μmg(x1+1)=Eka
得x1=
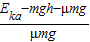 =
=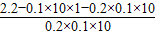 =5m
=5mb向右运动时,假设开始运动时到N的距离为x2,为了运动中不脱离轨道,最大高度在
 的圆周以下,然后返回,
的圆周以下,然后返回,同样当其通过光滑曲线轨道BN到达平台AB的左边速度为零时,所需轨道最短.
对b球,根据能量守恒得
μmg(2x2+x1+1)+mgh=Ekb
解得,x2=
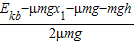 =2m
=2m则MN=x1+x2=7m
(2)a、b两球由于运动而损失的总机械能为△E=Eka+Ekb-2mgh=3.2J
答:
(1)符合要求的轨道MN的最短距离是7m;
(2)在满足(1)条件下,a、b两球由于运动而损失的总机械能是3.2J.
点评:本题的关键是分析什么条件下才能保证a、b在运动中不脱离平台与轨道,根据能量守恒进行处理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,质量为m1的物体甲通过三段轻绳悬挂,三段轻绳的结点为O.轻绳OB水平且B端与放置在水平面上的质量为m2的物体乙相连,轻绳OA与竖直方向的夹角θ=37°,物体甲、乙均处于静止状态.(取sin37°=0.6,cos37°=0.8,设最大静摩擦力等于滑动摩擦力)求:
如图所示,质量为m1的物体甲通过三段轻绳悬挂,三段轻绳的结点为O.轻绳OB水平且B端与放置在水平面上的质量为m2的物体乙相连,轻绳OA与竖直方向的夹角θ=37°,物体甲、乙均处于静止状态.(取sin37°=0.6,cos37°=0.8,设最大静摩擦力等于滑动摩擦力)求: 如图所示,ABMNCD为某个游戏场中的竖直固定轨道示意图,水平直轨道MN与右边半径R=3m的3/4光滑圆弧轨道NCD底端相连接,水平直轨道左边通过光滑曲线轨道BN与高为h=1m的平台AB相连接,平台AB长为1两个可视为质点的小球,两球质量均为0.lkg,开始时两球紧靠在一起,若同时给a、b一个初动能,使a向左运动,b向右运动,a的初动能为Eka=2.2J,b的初动能为Ekb=3.0J,设a、b与水平轨道、与平台之间的动摩擦因数u均为0.2.为使a、b在以后的运动中不脱离平台与轨道,可适当调节轨道MN的长度、小球a、b运动的初始位置.求
如图所示,ABMNCD为某个游戏场中的竖直固定轨道示意图,水平直轨道MN与右边半径R=3m的3/4光滑圆弧轨道NCD底端相连接,水平直轨道左边通过光滑曲线轨道BN与高为h=1m的平台AB相连接,平台AB长为1两个可视为质点的小球,两球质量均为0.lkg,开始时两球紧靠在一起,若同时给a、b一个初动能,使a向左运动,b向右运动,a的初动能为Eka=2.2J,b的初动能为Ekb=3.0J,设a、b与水平轨道、与平台之间的动摩擦因数u均为0.2.为使a、b在以后的运动中不脱离平台与轨道,可适当调节轨道MN的长度、小球a、b运动的初始位置.求 如图所示,电动势为E、内阻为r的电源与两个灯泡A、B及一个电阻R、理想电压表相接,开始时开关k断开,现在闭合开关k,下列表述正确的是( )
如图所示,电动势为E、内阻为r的电源与两个灯泡A、B及一个电阻R、理想电压表相接,开始时开关k断开,现在闭合开关k,下列表述正确的是( )