题目内容
13. 如图所示,两轻质弹簧a、b悬挂一质量为m的小球,整体处于平衡状态,a弹簧与竖直方向成30°角,b弹簧与竖直方向成60°角,a、b两弹簧的形变量相等,重力加速度为g,则( )
如图所示,两轻质弹簧a、b悬挂一质量为m的小球,整体处于平衡状态,a弹簧与竖直方向成30°角,b弹簧与竖直方向成60°角,a、b两弹簧的形变量相等,重力加速度为g,则( )| A. | 弹簧a、b的劲度系数之比为$\sqrt{3}$:1 | |
| B. | 弹簧a、b的劲度系数之比为$\sqrt{3}$:2 | |
| C. | 若弹簧a下端松脱,则松脱瞬间小球的加速度大小为$\sqrt{3}$g | |
| D. | 若弹簧b下端松脱,则松脱瞬间小球的加速度大小为$\frac{g}{2}$ |
分析 对小球受力分析,受到重力和两个弹簧的弹力,根据平衡条件并运用合成法得到两个弹力之比,再结合胡克定律求解出伸长量之比,根据小球平衡由弹簧松脱得出弹力变化情况,再据牛顿第二定律分析加速度情况.
解答  解:由题可知,两个弹簧之间相互垂直,画出受力图如图,设弹簧的伸长量都是x:
解:由题可知,两个弹簧之间相互垂直,画出受力图如图,设弹簧的伸长量都是x:
A、由受力图知,弹簧a中弹力:Fa=mgcos30°=$\frac{\sqrt{3}}{2}$mg,据胡克定律a弹簧的劲度系数为:k1=$\frac{{F}_{a}^{\;}}{x}$=$\frac{\sqrt{3}mg}{2x}$;
弹簧b中弹力:Fb=mgcos60°=$\frac{1}{2}$mg,据胡克定律b弹簧的劲度系数为:k2=$\frac{{F}_{b}^{\;}}{x}$=$\frac{mg}{2x}$所以弹簧a、b劲度系数之比为 $\sqrt{3}$:1.故A正确,B错误;
C、弹簧a中弹力为 $\frac{\sqrt{3}mg}{2}$,若弹簧a的左端松脱,则松脱瞬间b弹簧的弹力不变,故小球所受重力和b弹簧弹力的合力与F1大小相等方向相反,故小球的加速度a=$\frac{{F}_{a}^{\;}}{m}$=$\frac{\sqrt{3}}{2}g$.故C错误;
D、弹簧b中弹力为 $\frac{1}{2}$mg,若弹簧b的左端松脱,则松脱瞬间a弹簧的弹力不变,故小球所受重力和a弹簧弹力的合力与F2大小相等方向相反,故小球的加速度a=$\frac{{F}_{b}^{\;}}{m}$=$\frac{1}{2}$g,故D正确.
故选:AD
点评 本题考查共点力平衡条件的运用,关键是作图,三力中两个力的合力一定与第三个力等值、反向、共线,知道一个弹簧弹力变化的瞬间,另一弹簧弹力保持不变.

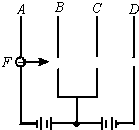 如图所示,从P处释放一个无初速度的电子向B板方向运动,指出下列对电子运动的描述中哪项是正确的(设电源电动势E)( )
如图所示,从P处释放一个无初速度的电子向B板方向运动,指出下列对电子运动的描述中哪项是正确的(设电源电动势E)( )| A. | 电子到达B板时的动能是Ee | B. | 电子从B板到达C板动能变化量为零 | ||
| C. | 电子到达D板时动能是2Ee | D. | 电子在A板和D板之间做往复运动 |
 如图所示,一个理想变压器原线圈和副线圈的匝数分别为n1和n2,正常工作时输入和输出的电压分别为U1和U2,已知n1>n2,则( )
如图所示,一个理想变压器原线圈和副线圈的匝数分别为n1和n2,正常工作时输入和输出的电压分别为U1和U2,已知n1>n2,则( )| A. | 该变压器为降压变压器,U1>U2 | B. | 该变压器为降压变压器,U2>U1 | ||
| C. | 该变压器为升压变压器,U1>U2 | D. | 该变压器为升压变压器,U2>U1 |
 如图所示,在动摩擦因数μ=0.2的水平面上有一个质量m=lkg的小球,小球左侧连接一水平轻弹簧,弹簧左端固定在墙上,右侧连接一与竖直方向成θ=45°角的不可伸长的轻绳,轻绳另一端固定在天花板上,此时小球处于静止状态,且水平面对小球的弹力恰好为零.在剪断轻绳的瞬间(g取10m/s2),下列说法中正确的是( )
如图所示,在动摩擦因数μ=0.2的水平面上有一个质量m=lkg的小球,小球左侧连接一水平轻弹簧,弹簧左端固定在墙上,右侧连接一与竖直方向成θ=45°角的不可伸长的轻绳,轻绳另一端固定在天花板上,此时小球处于静止状态,且水平面对小球的弹力恰好为零.在剪断轻绳的瞬间(g取10m/s2),下列说法中正确的是( )| A. | 小球受力个数不变 | |
| B. | 小球立即向左加速,且加速度的大小为a=8m/s2 | |
| C. | 小球立即向左加速,且加速度的大小为a=l0m/s2 | |
| D. | 若剪断的是弹簧,则剪断瞬间小球加速度的大小a=l0$\sqrt{2}$m/s2 |
 如图a所示,将质量为m的物体置于倾角为θ的平板上,当θ从0缓慢增大到90°的过程中,物体所受摩擦力Ff与θ的关系如图b所示,已知物体始终没有脱离平板,物体与平板间的动摩擦因数为0.75.最大静摩擦力与滑动摩擦力相等,重力加速度为g,则( )
如图a所示,将质量为m的物体置于倾角为θ的平板上,当θ从0缓慢增大到90°的过程中,物体所受摩擦力Ff与θ的关系如图b所示,已知物体始终没有脱离平板,物体与平板间的动摩擦因数为0.75.最大静摩擦力与滑动摩擦力相等,重力加速度为g,则( )| A. | O-q段图线是直线 | B. | q-$\frac{π}{2}$段图线是直线 | ||
| C. | P=$\frac{3mg}{5}$ | D. | q=$\frac{π}{6}$ |
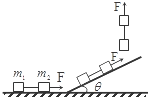 如图所示,质量为m1和m2的两个材料相同的物体用细线相连,在大小恒定的拉力F作用下,先沿水平面,再沿斜面,最后竖直向上匀加速运动,不计空气阻力,在三个阶段的运动中,线上拉力的大小( )
如图所示,质量为m1和m2的两个材料相同的物体用细线相连,在大小恒定的拉力F作用下,先沿水平面,再沿斜面,最后竖直向上匀加速运动,不计空气阻力,在三个阶段的运动中,线上拉力的大小( )| A. | 由大变小 | B. | 由小变大 | ||
| C. | 始终不变且大小为$\frac{m}{{m}_{1}+{m}_{2}}$F | D. | 由大变小再变大 |
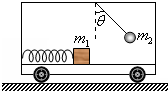 在水平地面上运动的小车车厢底部有一质量为m1的木块,木块和车厢通过一根轻质弹簧相连接,弹簧的劲度系数为k.在车厢的顶部用一根细线悬挂一质量为m2的小球.某段时间内发现细线与竖直方向的夹角为θ,在这段时间内木块与车厢始终保持相对静止,如图所示.不计木块与车厢底部的摩擦力,则在这段时间内弹簧处在拉伸(选填“压缩”或“拉伸”)状态,形变量为$\frac{{{m_1}gtanθ}}{k}$.
在水平地面上运动的小车车厢底部有一质量为m1的木块,木块和车厢通过一根轻质弹簧相连接,弹簧的劲度系数为k.在车厢的顶部用一根细线悬挂一质量为m2的小球.某段时间内发现细线与竖直方向的夹角为θ,在这段时间内木块与车厢始终保持相对静止,如图所示.不计木块与车厢底部的摩擦力,则在这段时间内弹簧处在拉伸(选填“压缩”或“拉伸”)状态,形变量为$\frac{{{m_1}gtanθ}}{k}$.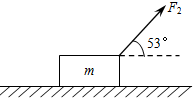 质量m=20kg的木箱放在水平地面上,木箱与地面之间的动摩擦因数μ=0.5.若用水平力F1拉木箱,木箱恰好做匀速直线运动;若用F2=150N、与水平方向成53°斜向上的拉力作用于静止的木箱上,如图所示,作用时间4s后撤去F2.求:
质量m=20kg的木箱放在水平地面上,木箱与地面之间的动摩擦因数μ=0.5.若用水平力F1拉木箱,木箱恰好做匀速直线运动;若用F2=150N、与水平方向成53°斜向上的拉力作用于静止的木箱上,如图所示,作用时间4s后撤去F2.求: 如图,用两根绳子把质量为10千克的物体W吊在水平杆子AB上,∠ACW=150°,∠BCW=120°,如果绳子的质量忽略不计,求A处和B处所受力的大小.
如图,用两根绳子把质量为10千克的物体W吊在水平杆子AB上,∠ACW=150°,∠BCW=120°,如果绳子的质量忽略不计,求A处和B处所受力的大小.