题目内容
 如图,长为R的轻绳,上端固定在O点,下端连一个小球.小球接近地面,处于静止状态.现给小球一沿水平方向的初速度V0,小球开始做圆周运动.设小球到达最高点时绳突然断开.已知小球最后落在离小球最初位置3R的地面上.求小球的初速度V0,重力加速度为g.
如图,长为R的轻绳,上端固定在O点,下端连一个小球.小球接近地面,处于静止状态.现给小球一沿水平方向的初速度V0,小球开始做圆周运动.设小球到达最高点时绳突然断开.已知小球最后落在离小球最初位置3R的地面上.求小球的初速度V0,重力加速度为g.分析:球离开最高点后做平抛运动,根据平抛运动的位移公式列,小球从最低点到最高点过程,只有重力做功,根据机械能守恒定律列式,联立方程即可求解初速度.
解答:解:设小球质量为m,小球到达最高点时速度为V,由机械能守恒定律,得
mv02=
mv2+2mgR…①
绳子断开后,小球作平抛运动,经时间t到达地面
则3R=vt…②
2R=
gt2…③
由①②③式得v0=
答:小球的初速度为
.
| 1 |
| 2 |
| 1 |
| 2 |
绳子断开后,小球作平抛运动,经时间t到达地面
则3R=vt…②
2R=
| 1 |
| 2 |
由①②③式得v0=
| 5 |
| 2 |
| gR |
答:小球的初速度为
| 5 |
| 2 |
| gR |
点评:本题主要考查了机械能守恒定律及平抛运动基本公式的直接应用,难度不大,属于基础题.

练习册系列答案
相关题目
 如图所示,长为R的轻绳,上端固定在O点,下端连一小球.小球接近地面,处于静止状态.现给小球一沿水平方向的初速度v0=
如图所示,长为R的轻绳,上端固定在O点,下端连一小球.小球接近地面,处于静止状态.现给小球一沿水平方向的初速度v0=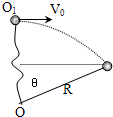 一质量为m的小球,系于长为R的轻绳的一端,绳的另一端固定在空间的O点,假定绳是不可伸长的、柔软且无弹性的.今把小球从O点的正上方离O点的距离为
一质量为m的小球,系于长为R的轻绳的一端,绳的另一端固定在空间的O点,假定绳是不可伸长的、柔软且无弹性的.今把小球从O点的正上方离O点的距离为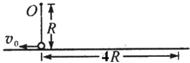 如图所示,长为R的轻绳,上端固定在O点,下端连接一只小球.小球接近地面,处于静止状态.现给小球一沿水平方向的初速度,小球开始在竖直平面内做圆周运动.设小球到达最高点时绳突然断开,已知小球最后落在离小球最初位置4R的地面上,重力加速度为g.试求:(图中所标 v0的数值未知)
如图所示,长为R的轻绳,上端固定在O点,下端连接一只小球.小球接近地面,处于静止状态.现给小球一沿水平方向的初速度,小球开始在竖直平面内做圆周运动.设小球到达最高点时绳突然断开,已知小球最后落在离小球最初位置4R的地面上,重力加速度为g.试求:(图中所标 v0的数值未知)