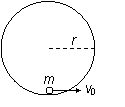题目内容
宇航员在某一未知星球表面完成下面实验:如图所示,在固定的竖直光滑圆弧轨道内部的最低点,有一质量为m的小球(可视为质点),现给小球水平初速度v0,使小球在竖直平面内做圆周运动,测得小球在最高点和最低点时所受压力大小分别为F1、F2.然后他在携带的资料中发现这样的信息:在该星球赤道上有相距路程为L的A、B两位置,当某一时刻阳光垂直照射A处时,B处的阳光与星球表面成θ角.请你帮他完成如下计算:
(1)求出该星球表面的重力加速度;
(2)求出该星球的第一宇宙速度.
(1)求出该星球表面的重力加速度;
(2)求出该星球的第一宇宙速度.

(1)由题意根据合力提供向心力:
在最低点:F1-mg=m
在最高点:F2+mg=m
根据机械能守恒得:
mv02=
mv2+mg2r
解得g=
故星球表面的重力加速度为
.
(2)根据A、B两点的日照情况可计算出该星球的半径R=
用v表示该星球的第一宇宙速度,有
mg=m
得v=
=
故星球的第一宇宙速度为
.
在最低点:F1-mg=m
| v02 |
| r |
在最高点:F2+mg=m
| v2 |
| r |
根据机械能守恒得:
| 1 |
| 2 |
| 1 |
| 2 |
解得g=
| F1-F2 |
| 6m |
故星球表面的重力加速度为
| F1-F2 |
| 6m |
(2)根据A、B两点的日照情况可计算出该星球的半径R=
| L | ||
|
用v表示该星球的第一宇宙速度,有
mg=m
| v2 |
| R |
得v=
| gR |
|
故星球的第一宇宙速度为
|

练习册系列答案
相关题目
 一宇航员在某未知星球的表面上做平抛运动实验:在离地面h高处让小球以v0的初速度水平抛出,他测出小球落地点与抛出点的水平距离为x,又已知该星球的半径为R,己知万有引力常量为G,求:
一宇航员在某未知星球的表面上做平抛运动实验:在离地面h高处让小球以v0的初速度水平抛出,他测出小球落地点与抛出点的水平距离为x,又已知该星球的半径为R,己知万有引力常量为G,求: (2011?椒江区模拟)宇航员在某一未知星球表面完成下面实验:如图所示,在固定的竖直光滑圆弧轨道内部的最低点,有一质量为m的小球(可视为质点),现给小球水平初速度v0,使小球在竖直平面内做圆周运动,测得小球在最高点和最低点时所受压力大小分别为F1、F2.然后他在携带的资料中发现这样的信息:在该星球赤道上有相距路程为L的A、B两位置,当某一时刻阳光垂直照射A处时,B处的阳光与星球表面成θ角.请你帮他完成如下计算:
(2011?椒江区模拟)宇航员在某一未知星球表面完成下面实验:如图所示,在固定的竖直光滑圆弧轨道内部的最低点,有一质量为m的小球(可视为质点),现给小球水平初速度v0,使小球在竖直平面内做圆周运动,测得小球在最高点和最低点时所受压力大小分别为F1、F2.然后他在携带的资料中发现这样的信息:在该星球赤道上有相距路程为L的A、B两位置,当某一时刻阳光垂直照射A处时,B处的阳光与星球表面成θ角.请你帮他完成如下计算: