题目内容
6．在光滑的水平面上，质量分别为2kg和1kg的A、B两个小球分别以0.5m/s和2m/s的速度相向运动，碰撞后两球粘在一起，则它们的共同速度大小为$\frac{1}{3}$m/s，方向与A球相反（填“相同”或“相反”）．分析 AB碰撞过程中，动量守恒，由动量守恒定律可以求出它们的共同速度．
解答 解：设A球的速度方向为正方向，根据动量守恒：m1v1-m2v2=（m1+m2）v
2×0.5-1×2=（2+1）v
得：v=-$\frac{1}{3}$m/s
即方向与A球的初速度方向相反．
故答案为：$\frac{1}{3}$；相反
点评 本题考查了完全非弹性碰撞过程，应用动量守恒定律即可正确解题，注意要规定正方向．
练习册系列答案
走进文言文系列答案
相关题目
3．在物理学发展的过程中，许多物理学家的科学发现推动了人类历史的进步．对以下几位物理学家所作科学贡献的表述中，与事实相符的是（ ）
| A． | 哥白尼提出了日心说并发现了行星沿椭圆轨道运行的规律 | |
| B． | 开普勒通过研究行星观测记录，发现了行星运动三大定律 | |
| C． | 笛卡尔根据理想斜面实验，提出了力不是维持物体运动的原因 | |
| D． | 牛顿首先将实验事实和逻辑推理（包括数学推演）和谐地结合起来 |
17．
如图，从地面上方某点，将一小球以10m/s的初速度沿水平方向抛出，小球经过1s落地，不计空气阻力，g=10m/s2，则可求出（ ）
如图，从地面上方某点，将一小球以10m/s的初速度沿水平方向抛出，小球经过1s落地，不计空气阻力，g=10m/s2，则可求出（ ）| A． | 小球抛出时离地面的高度是5m | |
| B． | 小球从抛出点到落地点的位移大小是10m | |
| C． | 小球落地时的速度大小是20m/s | |
| D． | 小球落地时的速度方向与水平地面成60°角 |
在某光电效应实验中，得到的遏止电压Uc与入射光的频率v的关系如图所示，若该直线的斜率为k，横轴截距为b，电子电荷量的绝对值为e，求：
1．有关物体的动量，下列说法正确的是（ ）
| A． | 某一物体的动量改变，一定是速度大小改变 | |
| B． | 某一物体的动量改变，一定是速度方向改变 | |
| C． | 某一物体的运动速度改变，其动量可能不变 | |
| D． | 物体的运动状态改变，其动量一定改变 |
11．两个均可视为点电荷的带电荷量分别为-Q和+5Q的相同金属小球固定在相距为r的两处，它们间库仑力的大小为F，若将两小球相互接触后将其固定距离变为0.5r，则两球间库仑力的大小为（ ）
| A． | $\frac{16}{5}F$ | B． | $\frac{5}{16}F$ | C． | $\frac{4}{5}F$ | D． | $\frac{1}{5}F$ |
18．
如图，一端接有定值电阻R的足够长的平行金属导轨，放在绝缘斜面上（斜面未画出），匀强磁场垂直于导轨平面向上，导体棒ab垂直于导轨放置．现给导体棒沿斜面向上的初速度v，经过一段时间导体棒又回到原位置．在运动过程中导体棒ab始终垂直于导轨，导轨和导体棒的电阻可忽略不计．则（ ）
如图，一端接有定值电阻R的足够长的平行金属导轨，放在绝缘斜面上（斜面未画出），匀强磁场垂直于导轨平面向上，导体棒ab垂直于导轨放置．现给导体棒沿斜面向上的初速度v，经过一段时间导体棒又回到原位置．在运动过程中导体棒ab始终垂直于导轨，导轨和导体棒的电阻可忽略不计．则（ ）| A． | 在上滑过程导体棒中的电流方向由a到b | |
| B． | 回到原位置时导体棒的速度大小仍为v | |
| C． | 开始上滑和回到原位置时导体棒的加速度大小相等 | |
| D． | 上滑过程与下滑到初始位置的过程通过导体棒截面的电荷量相等 |
15．
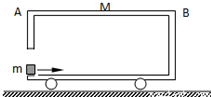如图所示，质量为M，长为L的车厢静止在光滑水平面上，此时质量为m的木块正以水平速度v从左边进入车厢板向右运动，车厢底板粗糙，m与右壁B发生无能量损失的碰撞后又被弹回，最后又恰好停在车厢左端点A，则以下叙述中正确的是（ ）
如图所示，质量为M，长为L的车厢静止在光滑水平面上，此时质量为m的木块正以水平速度v从左边进入车厢板向右运动，车厢底板粗糙，m与右壁B发生无能量损失的碰撞后又被弹回，最后又恰好停在车厢左端点A，则以下叙述中正确的是（ ）| A． | 该过程中产生的内能为$\frac{1}{2}$mv2 | |
| B． | 车厢底板的动摩擦因数为$\frac{{M{v^2}}}{4（m+M）gL}$ | |
| C． | M的最终速度为$\frac{mv}{m+M}$ | |
| D． | m、M最终速度为零 |
“测定玻璃的折射率”实验中，下图是在纸上留下的实验痕迹，其中直线a、a′是描在纸上的玻璃砖的两个边．