题目内容
10.根据波尔理论,氢原子的电子由外层轨道跃迁到内层轨道后,原子的能量减小,电子的动能增加,(填“增加”.“不变”.“减小”)若某原子的电子从能量为E的轨道跃迁到能量为E'的轨道,辐射出波长为λ的光,以h表示普朗克常量,c表示真空中的光速,则E'等于$E-h\frac{c}{λ}$.分析 氢原子的电子由外层轨道跃迁到内层轨道后,原子的能量减小,根据库仑引力提供向心力得出电子动能的变化.跃迁时辐射的光子能量等于两能级间的能级差,从而求出E′的大小.
解答 解:氢原子的电子由外层轨道跃迁到内层轨道后,原子的能量减小.
根据k$\frac{{e}^{2}}{{r}^{2}}=m\frac{{v}^{2}}{r}$知电子的动能为:${E}_{k}=\frac{1}{2}m{v}^{2}=\frac{1}{2}k\frac{{e}^{2}}{r}$,电子轨道半径减小,则电子动能增加.
根据$E-E′=h\frac{c}{λ}$得:$E′=E-h\frac{c}{λ}$.
故答案为:减小,增加,$E-h\frac{c}{λ}$.
点评 解决本题的关键知道高能级向低能级跃迁,辐射光子,从低能级向高能级跃迁,吸收光子.以及掌握能级差与光子频率的关系.同时知道激发态不稳定,会向基态发生跃迁,不同的能级间有不同的能极差,辐射的光子频率不同,最后掌握电子跃迁中,动能与电势能,及总能量如何变化.

练习册系列答案
相关题目
8.做匀速圆周运动的物体,下列说法正确的是( )
| A. | 线速度不变 | B. | 动能不变 | ||
| C. | 加速度不变 | D. | 物体做匀变速运动 |
1.弹簧振子做简谐运动,若某一过程中振子的速率在减小,则此时振子的运动( )
| A. | 速度与位移方向一定相反 | B. | 加速度与速度方向可能相同 | ||
| C. | 回复力一定在增大 | D. | 位移可能在减小 |
18. 如图所示,两个相同灯泡L1、L2分别与电阻R和自感线圈L串联,接到内阻不计的电源两端,闭合电键S,当电路稳定后,两灯泡均正常发光.已知自感线圈的自感系数很大,阻值与电阻R相同.下列说法正确的是( )
如图所示,两个相同灯泡L1、L2分别与电阻R和自感线圈L串联,接到内阻不计的电源两端,闭合电键S,当电路稳定后,两灯泡均正常发光.已知自感线圈的自感系数很大,阻值与电阻R相同.下列说法正确的是( )
 如图所示,两个相同灯泡L1、L2分别与电阻R和自感线圈L串联,接到内阻不计的电源两端,闭合电键S,当电路稳定后,两灯泡均正常发光.已知自感线圈的自感系数很大,阻值与电阻R相同.下列说法正确的是( )
如图所示,两个相同灯泡L1、L2分别与电阻R和自感线圈L串联,接到内阻不计的电源两端,闭合电键S,当电路稳定后,两灯泡均正常发光.已知自感线圈的自感系数很大,阻值与电阻R相同.下列说法正确的是( )| A. | 闭合S到电路稳定前,灯泡L1逐渐变亮 | |
| B. | 闭合S到电路稳定前,灯泡L2逐渐变亮 | |
| C. | 断开S的一段时间内,B点电势比A点电势低 | |
| D. | 断开S的一段时间内,灯泡L2亮一下后逐渐熄灭 |
15.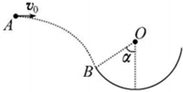 如图所示,B为半径为R的竖直光滑圆轨道的左端点,它和圆心O的连线与竖直方向的夹角为α.一个质量为m的小球在圆轨道左侧的A点以水平速度v0被抛出,恰好沿B点的切线方向进入圆轨道,已知重力加速度为g,下列说法正确的是( )
如图所示,B为半径为R的竖直光滑圆轨道的左端点,它和圆心O的连线与竖直方向的夹角为α.一个质量为m的小球在圆轨道左侧的A点以水平速度v0被抛出,恰好沿B点的切线方向进入圆轨道,已知重力加速度为g,下列说法正确的是( )
 如图所示,B为半径为R的竖直光滑圆轨道的左端点,它和圆心O的连线与竖直方向的夹角为α.一个质量为m的小球在圆轨道左侧的A点以水平速度v0被抛出,恰好沿B点的切线方向进入圆轨道,已知重力加速度为g,下列说法正确的是( )
如图所示,B为半径为R的竖直光滑圆轨道的左端点,它和圆心O的连线与竖直方向的夹角为α.一个质量为m的小球在圆轨道左侧的A点以水平速度v0被抛出,恰好沿B点的切线方向进入圆轨道,已知重力加速度为g,下列说法正确的是( )| A. | 小球从A运动到B的时间t=$\frac{{v}_{0}}{g}$tanα | |
| B. | A.B之间的距离L=$\frac{{v}_{0}^{2}}{g}$tanα(1+$\frac{tanα}{2}$) | |
| C. | 小球运动到B点时,重力的瞬时功率P=mgv0tanα | |
| D. | 小球运动到竖直圆轨道的最低点时,圆轨道对它的支持力F=$\frac{m{v}_{0}^{2}}{Rco{s}^{2}α}$+3mg-2mgcosα |
19.我国“神舟”系列飞船均由长征运载火箭发射,请回答火箭发射和神舟飞船回收的有关问题,下面说法正确的是( )
| A. | 火箭加速发射升空阶段,飞船内座椅对人的支持力大于人对座椅的压力 | |
| B. | 火箭加速发射升空阶段,飞船内人对座椅的作用力大于人的重力 | |
| C. | 神舟飞船减速下降阶段,人对座椅的压力小于人的重力 | |
| D. | 神舟飞船减速下降阶段,人对座椅的压力等于座椅对人的支持力 |
20.假设地球是一半径为R、质量分布均匀的球体.已知质量分布均匀的球壳对壳内物体的引力为零,地球表面的重力加速度为g.一矿井深度为d,则矿井底部的重力加速度为( )
| A. | 0 | B. | 1-$\frac{d}{R}$ | C. | g-$\frac{dg}{R}$ | D. | ($\frac{R-d}{R}$)2g |
 一个质点在水平面内运动的v-t图象如图所示,对应的a-t图象和x-t图象中正确的是( )
一个质点在水平面内运动的v-t图象如图所示,对应的a-t图象和x-t图象中正确的是( )


