题目内容
10.某兴趣实验小组在测定某电阻丝的电阻率时,从实验室中选择的实验器材有:螺旋测微器、米尺、内阻为1Ω的双量程电流表、内阻为5kΩ的双量程电压表、电动势为6.0V内阻可忽略不计的电源、最大阻值为20Ω的滑动变阻器、阻值约为5Ω的电阻丝、电建和若干导线.根据以上的实验器材回答下列问题:

(1)请根据自己设计的电路将图甲中的实物图连接完整.
(2)用螺旋测微器测量的电阻丝直径和用米尺测量的接入电路的电阻丝长度分别如图乙所示,则该电阻丝的直径d为1.850mm,电阻丝的长度L为30.50cm.在利用伏安法测量该电阻丝的阻值时,某次测量的电压表和电流表的示数如图丙所示,则该电阻丝两端的电压U为2.20V,流过电阻丝的电流I为0.44A.
(3)由以上测量的数据可得电阻丝的电阻率是4.4×10-5Ω•m(结果保留1位小数).
分析 (1)根据电源电动势大小选择电压表量程;根据I=$\frac{U}{{R}_{x}}$求出通过电流表的最大电流来选择电流表量程;根据电压表内阻远大于待测电阻可知电流表应选外接法;根据待测电阻小于变阻器全电阻可知变阻器可以用限流式接法.
(2)明确各种仪器的读数原理和估读要求,对刻度尺、电流表及电压表:
若最小分度出现“1”则可以估读到最小刻度的$\frac{1}{10}$;若最小分度出现“2”则应估读到最小分度的$\frac{1}{2}$;若最小分度出现“5”则应估读到最小分度的$\frac{1}{5}$,对螺旋测微器读数时注意半毫米刻度线,以及估读到0.001mm即可;
(3)根据电阻定律列式,利用(2)中数据即可求解.
解答 解:(1)由于金属丝的电阻比电压表的内阻小得多,因此采用电流表外接法;由于金属丝的电阻比滑动变阻器的总电阻要小,因此采用限流式接法,为了保证滑动变阻器起限流作用,滑动变阻器应该连接“B、C”或“A、D”几个接线柱;由题图可以看出电流表应该连接“-”接线柱和“0.6”接线柱,具体连线如图所示.
(2)由图可以看出:电压表的量程是3 V,最小分度为0.1V,所以读数是2.20 V;电流表的量程是0.6 A,最小分度为0.02A,所以读数是0.44 A;
由于螺旋测微器的半毫米刻度线已经露出,因此读数是1.850×10-3 m;
米尺的读数是40.50 cm-10.00 cm=30.50 cm.
(3)由电阻定律得
ρ=$\frac{RS}{l}$=$\frac{Uπ{d}^{2}}{IL}$=4.4×10-5Ω•m
故答案为:(1)如图所示; (2)1.850mm;30.50cm;2.20V;0.44A;(3)4.4×10-5Ω•m
点评 本题考查测量电动势和内电阻的实验,要明确:
(1)应掌握电学实验中,要通过估算来选择仪器,注意伏安法时电流表内外接法的选择方法,以及滑动变阻器采用分压和限流接法的要求.
(2)应掌握电压表与电流表读数方法以及“十分之一”、“五分之一”、“二分之一”估读的含义,并掌握螺旋测微器的使用及读数.
(3)根据电阻定律求电阻率.

 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案| A. | 牛顿最早指出力不是维持物体运动的原因 | |
| B. | 一个运动的物体,如果不再受力了,它总会逐渐停下来,这说明,静止状态才是物体长时间不受力时的“自然状态” | |
| C. | 伽利略根据理想实验推论出,如果没有摩擦,在水平面上的物体,一旦具有某一个速度,将保持这个速度继续运动下去 | |
| D. | 车速越大,刹车后滑行的路程越长,所以惯性越大 |
 如图的伏安特性曲线甲、乙分别反映了电源1、2的外电压随流过电源的电流变化规律,电源1、2的内阻分别用r1、r2表示,现将2个阻值相同的电阻R分别接在电源1、2的两端,电路中的电流分别用I1、I2表示,此时电源1、2的输出功率分别用P1、P2表示,两电源的效率分别用η1、η2表示,下列选项中正确的是( )
如图的伏安特性曲线甲、乙分别反映了电源1、2的外电压随流过电源的电流变化规律,电源1、2的内阻分别用r1、r2表示,现将2个阻值相同的电阻R分别接在电源1、2的两端,电路中的电流分别用I1、I2表示,此时电源1、2的输出功率分别用P1、P2表示,两电源的效率分别用η1、η2表示,下列选项中正确的是( )| A. | r1>r2,I1>I2 | B. | r1>r2,I1<I2 | C. | P1>P2,η1<η2 | D. | P1<P2,η1<η2 |
 如图所示,在x轴上相距为L的两点固定两个等量异种点电荷+Q、-Q,虚线是以+Q所在点为圆心、$\frac{L}{2}$为半径的圆,a、b、c、d是圆上的四个点,其中a、c两点在x轴上,b、d两点关于x轴对称.则下列判断正确的是( )
如图所示,在x轴上相距为L的两点固定两个等量异种点电荷+Q、-Q,虚线是以+Q所在点为圆心、$\frac{L}{2}$为半径的圆,a、b、c、d是圆上的四个点,其中a、c两点在x轴上,b、d两点关于x轴对称.则下列判断正确的是( )| A. | 四个点中c点处的电势最低,a 点电势最高 | |
| B. | b、d两点处的电场强度相同、电势相同 | |
| C. | b、d两点处的电场强度相同、电势不相同 | |
| D. | 将一试探电荷-q沿圆周由a点移至c点,-q的电势能增加 |
 在如图所示的电路中,电源内阻不可忽略,在调节可变电阻R的阻值过程中,发现理想电压表的示数减小,则( )
在如图所示的电路中,电源内阻不可忽略,在调节可变电阻R的阻值过程中,发现理想电压表的示数减小,则( )| A. | R的阻值变大 | B. | 路端电压不变 | ||
| C. | 干路电流减小 | D. | 外电路的总电阻减小 |
(1)弹簧自然悬挂,待弹簧静止时,长度记为L0;弹簧下端挂上砝码盘时,长度记为Lx;在砝码盘中每次增加10g砝码,弹簧长度依次记为L1至L6.数据如下表.
| 代表符号 | L0 | Lx | L1 | L2 | L3 | L4 | L5 | L6 |
| 数值(cm) | 25.35 | 27.35 | 29.35 | 31.30 | 33.40 | 35.35 | 37.40 | 39.30 |
(2)如图所示是该同学根据表中数据作的图,纵轴是砝码的质量,横轴是弹簧长度与Lx的差值(填“L0”或“Lx”).

(3)由图可知弹簧的劲度系数为4.9N/m;通过图和表可知砝码盘的质量为10g.(结果保留两位有效数字,重力加速度g取9.8m/s2)

 现要验证“当质量一定时,物体运动的加速度与它所受的合外力成正比”这一物理规律.给定的器材如下:一倾角可以调节的长斜面(如图)、小车、计时器一个、米尺.
现要验证“当质量一定时,物体运动的加速度与它所受的合外力成正比”这一物理规律.给定的器材如下:一倾角可以调节的长斜面(如图)、小车、计时器一个、米尺.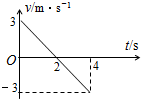 你可能到公园或游乐园蹦床.如图所示是一同学某次蹦床跳起后的v-t图象,结合你的体会和经历,回答下列问题:
你可能到公园或游乐园蹦床.如图所示是一同学某次蹦床跳起后的v-t图象,结合你的体会和经历,回答下列问题: