��Ŀ����
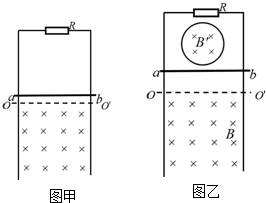
2�� ��ͼ��ʾ������Ϊm�Ŀ�Ӹ�ab������Ħ������ˮƽ�ĵ��컬�У�������ΪL�����������R���ӣ�������ֱ���µ���ǿ�ų��У��Ÿ�ǿ��ΪB���˴�x��ԭ��O�Դ�СΪv0��ˮƽ���ٶ����һ��У�ֱ����ֹ����֪���������˶��������ٶ�v��λ��x�ĺ�����ϵ�ǣ�v=v0-B2L2$\frac{x}{mR}$���˼�����ĵ�������ƣ�
��ͼ��ʾ������Ϊm�Ŀ�Ӹ�ab������Ħ������ˮƽ�ĵ��컬�У�������ΪL�����������R���ӣ�������ֱ���µ���ǿ�ų��У��Ÿ�ǿ��ΪB���˴�x��ԭ��O�Դ�СΪv0��ˮƽ���ٶ����һ��У�ֱ����ֹ����֪���������˶��������ٶ�v��λ��x�ĺ�����ϵ�ǣ�v=v0-B2L2$\frac{x}{mR}$���˼�����ĵ�������ƣ���1����������ܵİ�����F����λ��x�仯�ĺ���ʽ��
��2������˿�ʼ�˶���ֹͣ�˶�������ͨ��R�ĵ�����
��3����ӿ�ʼ��������λ��Ϊȫ��һ��ʱ��·�в����Ľ����ȣ�
���� ��1�����ڴų��������˶�ʱ���и�Ÿ��߲�����Ӧ�������ܵ�����İ����������ã�����F=BIL��I=$\frac{BLv}{R}$���Լ��˵��ٶ�v��λ��x�ĺ�����ϵʽv=v0-B2L2$\frac{x}{mR}$���������ɵõ�������F����λ��x�仯�ĺ���ʽ��
��2�����ݶ��������͵�����ʽq=It������q��
��3�������������һ��λ��ʱ���ٶȣ������˶������У��˼��ٵĶ�����ȫת��Ϊ����R�����������������غ�������R����������Q��
��� �⣺��1�����ڴų��������˶�ʱ�����ܵİ�����Ϊ��F=BIL�����У�I=$\frac{BLv}{R}$��
�����⣬�˵��ٶ�v��λ��x�ĺ�����ϵΪ��v=v0-B2L2$\frac{x}{mR}$��
������F=$\frac{{B}_{\;}^{2}{L}_{\;}^{2}}{R}$v=$\frac{{B}_{\;}^{2}{L}_{\;}^{2}}{R}$��v0-B2L2$\frac{x}{mR}$��
����ʽ��֪��������F��λ��x�����Թ�ϵ��
��2�����ݶ��������ã�-B$\overline{I}$L��t=0-mv0��
����q=I��t=$\frac{m{v}_{0}^{\;}}{BL}$
��3����v=0ʱ��$x=\frac{mR{v}_{0}^{\;}}{{B}_{\;}^{2}{L}_{\;}^{2}}$
��$x��=\frac{x}{2}$ʱ��$v={v}_{0}^{\;}-{B}_{\;}^{2}{L}_{\;}^{2}��\frac{1}{mR}��\frac{1}{2}��\frac{mR{v}_{0}^{\;}}{{B}_{\;}^{2}{L}_{\;}^{2}}$=$\frac{{v}_{0}^{\;}}{2}$
���������غ㣺${Q}_{1}^{\;}=\frac{1}{2}m{v}_{0}^{2}-\frac{1}{2}m��\frac{{v}_{0}^{\;}}{2}��_{\;}^{2}=\frac{3}{8}m{v}_{0}^{2}$
�𣺣�1�������ܵİ�����F����λ��x�仯�ĺ���ʽΪF=$\frac{{B}_{\;}^{2}{L}_{\;}^{2}}{R}$��v0-B2L2$\frac{x}{mR}$����
��2���˿�ʼ�˶���ֹͣ�˶�������ͨ��R�ĵ���qΪ=$\frac{m{v}_{0}^{\;}}{BL}$��
��3���˿�ʼ�˶���ֹͣ�˶������е���R����������QΪ$\frac{3}{8}m{v}_{0}^{2}$
���� �����е�Ÿ�Ӧ����ѧ���⣬�����ͼ��㰲�����ǽ���Ĺؼ������������غ㡢ŷķ���ɡ������ڵ�Ÿ�Ӧ���ɼ��������������ص���з�������⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| A�� | �ʵ��ڵ�1��ĩֹͣ�˶� | B�� | �ʵ���ǰ2���ڵ�λ��Ϊ�� | ||
| C�� | �ʵ��ڵ�1��ĩ�ı��˶����� | D�� | �ʵ��ڵ�2�����������˶� |
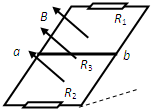 ��б�⻬���㹻����ƽ�е��촦����ǿ�ų��У������ϵĵ���R1=3�����±߽�һ������Ϊ6���Ļ���������R2��������ab������Ϊm������R3=4����������費�ƣ�б���б��Ϊ�����������ab���ŵ�������»��Ĺ����У�������
��б�⻬���㹻����ƽ�е��촦����ǿ�ų��У������ϵĵ���R1=3�����±߽�һ������Ϊ6���Ļ���������R2��������ab������Ϊm������R3=4����������費�ƣ�б���б��Ϊ�����������ab���ŵ�������»��Ĺ����У�������| A�� | �������˷����������Ĺ��������е�ܵļ����� | |
| B�� | �����Ͱ������Խ���������֮�͵��ڽ��������ӵĶ��ܡ���·����������֮�� | |
| C�� | ���������������·�ĵ���ԽС�������������˶�ʱ�ܵ��İ�����Խ�� | |
| D�� | �ı们�������������·�ĵ��裬�������������˶���R1�ĵ繦�����ʱ��R1��R2��R3�Ĺ���֮��ΪP1��P2��P3=2��1��6 |
 ��ͼ��ʾ��������Ϊq�������ɿ����ӵصĴ�����壬�������Ƶ������ֵ�ɲ����ĵ糡������q��������ľ���Ϊd����ô����q�ܵ��ĵ糡��Ϊ��������
��ͼ��ʾ��������Ϊq�������ɿ����ӵصĴ�����壬�������Ƶ������ֵ�ɲ����ĵ糡������q��������ľ���Ϊd����ô����q�ܵ��ĵ糡��Ϊ��������| A�� | k$\frac{{q}^{2}}{{d}^{2}}$ | B�� | k$\frac{{q}^{2}}{2{d}^{2}}$ | ||
| C�� | k$\frac{{q}^{2}}{4{d}^{2}}$ | D�� | ���������𰸾����� |

| A�� | С������״��ʹ�֮��Ķ�Ħ������������֮���С | |
| B�� | �����ʹ���С����������� | |
| C�� | �����ڼ״��ʹ��ϵ�����������ƽ�����ʱ������ϵĴ� | |
| D�� | �����ʹ�����С����Ħ��������������� |
 ����Ϊ��m=1Kg�������㹻����ľ����ڹ⻬��ˮƽ���ϣ��Ҷ˵���ֱ����ľ���L=0.08m������һ����ҲΪm�Ļ�����v0=3m/s��ˮƽ�ٶȴӰ����˻���ľ�壬������ľ����Ħ��ϵ��Ϊ��=0.1�������뵵��ʼ��δ��ײ��ľ���뵵�������ٶȴ�С���䣬�����෴������ײʱ�伫�̣����Բ��ƣ���ľ����ײ3�κ�ľ���뻬���Ѵﵽ��ͬ�ٶȣ�ľ���뵵�干��4�Σ�������ľ���Ϸ�����Ե�ʱ����3s����Ի���������4.5m��
����Ϊ��m=1Kg�������㹻����ľ����ڹ⻬��ˮƽ���ϣ��Ҷ˵���ֱ����ľ���L=0.08m������һ����ҲΪm�Ļ�����v0=3m/s��ˮƽ�ٶȴӰ����˻���ľ�壬������ľ����Ħ��ϵ��Ϊ��=0.1�������뵵��ʼ��δ��ײ��ľ���뵵�������ٶȴ�С���䣬�����෴������ײʱ�伫�̣����Բ��ƣ���ľ����ײ3�κ�ľ���뻬���Ѵﵽ��ͬ�ٶȣ�ľ���뵵�干��4�Σ�������ľ���Ϸ�����Ե�ʱ����3s����Ի���������4.5m�� ��ͼ��ʾ���̶����õ����⻬ƽ�н������죬���d=0.2m���������ϵIJ�����ˮƽ�ģ����ڴŸ�Ӧǿ��B=0.1T��������ֱ���µ��н�ų��У�����R=3���������H=0.8m��������ab����m=0.2kg������r=1�����ڵ����Ͼ�����h=0.2m�ĸߴ��ɾ�ֹ�ͷţ��˶�������a��b����ʼ���뵼��Ӵ����ò��Ҹ߶���ͬ����ص���������Ե��ˮƽ����s=0.4m��g=10m/s2����
��ͼ��ʾ���̶����õ����⻬ƽ�н������죬���d=0.2m���������ϵIJ�����ˮƽ�ģ����ڴŸ�Ӧǿ��B=0.1T��������ֱ���µ��н�ų��У�����R=3���������H=0.8m��������ab����m=0.2kg������r=1�����ڵ����Ͼ�����h=0.2m�ĸߴ��ɾ�ֹ�ͷţ��˶�������a��b����ʼ���뵼��Ӵ����ò��Ҹ߶���ͬ����ص���������Ե��ˮƽ����s=0.4m��g=10m/s2����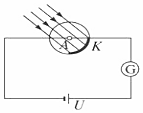 ��Ƶ��δ֪������������ij���ܵ�����ʱ���й���ӷɳ����ָ���һ����ѹ�ɵ��ҿ�ָʾ��ѹ��ֵ��ֱ����Դ��һ�������Ⱥܸߵ����������ƣ�����ͼ�ķ��������һ�ֵ�·�������ѻ�������Ҫ���øõ�·����������������������ܵ�����ʱ�����Ĺ���ӵ��������ܣ���������Ƶĵ�·����Ҫ�IJ����Լ���Ҫ��¼�������ǵ��ӷ����ѹʱ�����ڻ�����ͷP��ʹ�����Ƶ�ʾ��Ϊ�㣬��¼��ʱ��ѹ����ʾ��U�����������Ĺ���ӵ�����������eU����֪���ӵ����Ϊe����
��Ƶ��δ֪������������ij���ܵ�����ʱ���й���ӷɳ����ָ���һ����ѹ�ɵ��ҿ�ָʾ��ѹ��ֵ��ֱ����Դ��һ�������Ⱥܸߵ����������ƣ�����ͼ�ķ��������һ�ֵ�·�������ѻ�������Ҫ���øõ�·����������������������ܵ�����ʱ�����Ĺ���ӵ��������ܣ���������Ƶĵ�·����Ҫ�IJ����Լ���Ҫ��¼�������ǵ��ӷ����ѹʱ�����ڻ�����ͷP��ʹ�����Ƶ�ʾ��Ϊ�㣬��¼��ʱ��ѹ����ʾ��U�����������Ĺ���ӵ�����������eU����֪���ӵ����Ϊe����