题目内容
8. 如图所示,高台的上面有一竖直的$\frac{1}{4}$圆弧形光滑轨道,半径R=1.25m,轨道端点B的切线水平.质量m=0.5kg的滑块(可视为质点)由轨道顶端A由静止释放,离开B点后经时间t=1s撞击在足够长的斜面上的P点.已知斜面的倾角θ=37°,斜面底端C与B点的水平距离x0=3m.当滑块m离开B点时,位于斜面底端C点、质量M=1kg的小车,在沿斜面向上的恒定拉力F作用下,由静止开始向上加速运动,恰好在P点被m击中并卡于其中.滑块与小车碰撞时间忽略不计,碰后立即撤去拉力F,此时小车整体速度变为3.2m/s,仍沿斜面向上运动.已知小车与斜面间动摩擦因数μ=0.25.g取10m/s2,sin37°=0.6,cos37°=0.8,不计空气阻力.求:
如图所示,高台的上面有一竖直的$\frac{1}{4}$圆弧形光滑轨道,半径R=1.25m,轨道端点B的切线水平.质量m=0.5kg的滑块(可视为质点)由轨道顶端A由静止释放,离开B点后经时间t=1s撞击在足够长的斜面上的P点.已知斜面的倾角θ=37°,斜面底端C与B点的水平距离x0=3m.当滑块m离开B点时,位于斜面底端C点、质量M=1kg的小车,在沿斜面向上的恒定拉力F作用下,由静止开始向上加速运动,恰好在P点被m击中并卡于其中.滑块与小车碰撞时间忽略不计,碰后立即撤去拉力F,此时小车整体速度变为3.2m/s,仍沿斜面向上运动.已知小车与斜面间动摩擦因数μ=0.25.g取10m/s2,sin37°=0.6,cos37°=0.8,不计空气阻力.求:(1)滑块离开至B点时的速度大小;
(2)拉力F大小;
(3)小车在碰撞后在斜面上运动的时间.
分析 (1)由机械能守恒定律求出滑块到达B点时的速度.
(2)由平抛运动知识求出M的水平位移,然后由几何知识求出M的位移,由运动学公式求出M的加速度,由牛顿第二定律求出拉力大小.
(3)由牛顿第二定律求出加速度,由运动学公式可以求出滑块的运动时间.
解答 解:(1)m由A到B过场中,由机械能守恒定律得:mgR=$\frac{1}{2}m{v}_{B}^{2}$
解得:vB=5m/s
(2)m离开B后做平抛运动的水平位移x=vBt=5m
由几何关系可得M的位移为:s=$\frac{x-{x}_{0}}{cos37°}$=$\frac{5-3}{0.8}m=2.5m$
设滑块M向上运动的加速度为a,由s=$\frac{1}{2}a{t}^{2}$
可得a=5m/s2
由牛顿第二定律可得:F-Mgsin37°-μMgcos37°=Ma
解得:F=13N
(3)撤去拉力后,滑块M沿斜面上滑过程的加速度:
(M+m)gsin37°+μ(M+m)gcos37°=(M+m)a1
a1=gsin37°+μgcos37°=8m/s2
上滑时间t1=$\frac{v}{{a}_{1}}=\frac{3.2}{8}s=0.4s$
上滑位移s1=$\frac{{v}^{2}}{2{a}_{1}}=\frac{3.{2}^{2}}{2×8}s$=0.64m
滑块M沿斜面下滑过程的加速度a2=gsin37°-μgcos37°=4m/s2
下滑过程s+s1=$\frac{1}{2}{a}_{2}{t}_{2}^{2}$
解 得:${t_2}=\sqrt{\frac{{2({s+{s_1}})}}{a_2}}=\sqrt{\frac{{2({2.5+0.64})}}{4}}s=1.25s$
所以返回所用的时间为:t=t1+t2=(0.4+1.25)s=1.65s
答:(1)滑块离开至B点时的速度大小5m/s;
(2)拉力F大小13N;
(3)小车在碰撞后在斜面上运动的时间1.65s.
点评 本题是多体多过程问题,分析清楚物体运动过程是正确解题的关键,应用机械能守恒定律、牛顿定律、运动学公式即可正确解题.

 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
| A. | 同一温度下,氧气分子速率呈现出“中间多、两头少”的分布规律 | |
| B. | 随着温度升高,每一个氧气分子的速率都增大 | |
| C. | 温度越高,分子的热运动越剧烈 | |
| D. | 随着温度的升高,氧气分子的平均动能一定增大 |
| A. | $\frac{{v}_{1}}{{v}_{2}}$=$\frac{R+{h}_{1}}{R+{h}_{2}}$ | B. | $\frac{{a}_{1}}{{a}_{2}}$=$\frac{(R+{h}_{2})^{2}}{(R+{h}_{1})^{2}}$ | ||
| C. | $\frac{{a}_{1}}{{a}_{2}}$=$\frac{R+{h}_{1}}{R+{h}_{2}}$ | D. | $\frac{{v}_{1}}{v}$=$\sqrt{\frac{R+{h}_{1}}{R}}$ |
 从发现情况到采取相应行动经过的时间叫做反应时间,用如图所示的方法可以研究人的反应时间.小强看到小龙松开直尺就立即抓住直尺,若小强做握尺准备时,手指位置指示在刻度尺20.00cm处,尺子下落后握住尺的位置指示在40.00cm处,则( )
从发现情况到采取相应行动经过的时间叫做反应时间,用如图所示的方法可以研究人的反应时间.小强看到小龙松开直尺就立即抓住直尺,若小强做握尺准备时,手指位置指示在刻度尺20.00cm处,尺子下落后握住尺的位置指示在40.00cm处,则( )| A. | 测得小强的反应时间约为0.14s | B. | 测得小强的反应时间约为0.20s | ||
| C. | 测得小龙的反应时间约为0.14s | D. | 测得小龙的反应时间约为0.20s |
 如图所示,理想变压器初级圈接一正弦交流电源,交变电压的有效值恒定不变.则下列说法中正确的是( )
如图所示,理想变压器初级圈接一正弦交流电源,交变电压的有效值恒定不变.则下列说法中正确的是( )| A. | 只将S1从2拨向1时,电流表示数变小 | |
| B. | 只将S2从4拨向3时,电流表示数变大 | |
| C. | 只将S3从闭合变为断开,电阻R2两端电压增大 | |
| D. | 只将变阻器R3的滑动触头上移,变压器的输入功率减小 |
 如图所示,一根两端开口、横截面积为S=2cm2足够长的玻璃管竖直插入水银槽中并固定(插入水银槽中的部分足够深).管中有一个质量不计的光滑活塞,活塞下封闭着长L=21cm的气柱,气体的温度t1=7℃,外界大气压取P0=1.0×105 Pa(相当于75cm汞柱高的压强).
如图所示,一根两端开口、横截面积为S=2cm2足够长的玻璃管竖直插入水银槽中并固定(插入水银槽中的部分足够深).管中有一个质量不计的光滑活塞,活塞下封闭着长L=21cm的气柱,气体的温度t1=7℃,外界大气压取P0=1.0×105 Pa(相当于75cm汞柱高的压强).
 某实验小组利用如图所示的装置探究功和动能变化的关系,他们将宽度为d的挡光片固定在小车上,用不可伸长的细线将其通过一个定滑轮与砝码盘相连,在水平桌面上的A、B两点各安装一个光电门,记录小车通过A、B时的遮光时间,小车中可以放置砝码.
某实验小组利用如图所示的装置探究功和动能变化的关系,他们将宽度为d的挡光片固定在小车上,用不可伸长的细线将其通过一个定滑轮与砝码盘相连,在水平桌面上的A、B两点各安装一个光电门,记录小车通过A、B时的遮光时间,小车中可以放置砝码.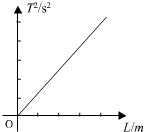 在“用单摆测定重力加速度的实验中”
在“用单摆测定重力加速度的实验中”