题目内容
14.如图甲的xoy坐标系中,第一、二和三象限中存在垂直于纸面向里的匀强磁场,磁感应强度为B.在O处有一粒子源,能向平面内各个方向均匀发射速率为v0的带正电的相同粒子,这些粒子与-x轴的最远交点为A(-2a,0).不计粒子重力以及粒子之间的相互作用.
(1)求粒子的比荷$\frac{q}{m}$.
(2)若在x=-1.5a处垂直于x轴放置一块足够长的荧光板MN,当粒子击中MN时将被吸收,并使荧光物质发光变亮.求MN上亮线的长度
(3)若撤去粒子源和第一象限内的磁场,在第四象限内加一个沿+y方向的场强为E=v0B的匀强电场,并在第一象限内x=3a处放一个足够长的荧光屏PQ,如图乙.在y轴上y=2a以下位置水平沿-x方向以速度v0发射上述粒子,则应在何处发射,才能使粒子击中PQ时的位置离P最远?求出最远距离.
分析 (1)在磁场中,根据洛伦兹力提供向心力几何几何关系即可求解;
(2)根据几何关系分别求出MN上粒子打中的最高点C和最低点离x轴的距离,从而求出亮线的长度;
(3)粒子在电场中做类平抛运动,根据平抛运动的基本公式求出击中点离P点的距离的表达式,再结合数学知识求解.
解答 
 解:(1)在磁场中,根据洛伦兹力提供向心力得:
解:(1)在磁场中,根据洛伦兹力提供向心力得:
Bqv0=m$\frac{{v}_{0}^{2}}{r}$
由几何关系得:r=a,
解得:$\frac{q}{m}$=$\frac{{v}_{0}}{Ba}$;
(2)MN上粒子打中的最高点C离x轴的距离:
l1=$\sqrt{(2a)^{2}-(\frac{3}{2}a)^{2}}$=$\frac{\sqrt{7}}{2}$a,
MN上粒子打中的最低点D离x轴的距离:
l2=$\sqrt{{a}^{2}-(1.5a-a)^{2}}$=$\frac{\sqrt{3}}{2}$a,
所以亮线的长度:
l=l1+l2=$\frac{\sqrt{7}+\sqrt{3}}{2}a$;
(3)粒子从y=-h处F点进入电场,
在电场中:x=v0t,h=$\frac{1}{2}$$\frac{qE}{m}$t2,
速度偏角为α,则tanα=$\frac{\frac{qE}{m}t}{{v}_{0}}$,
击中点离P点的距离为:Y=(3a-x)tanα,
联立各式解得:Y=3$\sqrt{2ah}$-2h,当$\sqrt{h}$=-$\frac{3\sqrt{2}a}{4}$,
即h=$\frac{9}{8}$a时,亦即发射点为y=$\frac{7}{8}$a时,
有:Ymax=3$\sqrt{2a•\frac{9}{8}h}$-2•$\frac{9a}{8}$=$\frac{9}{4}$a.
答:(1)粒子的比荷$\frac{q}{m}$为$\frac{{v}_{0}}{Ba}$;
(2)MN上亮线的长度为$\frac{\sqrt{7}+\sqrt{3}}{2}a$;
(3)发射点为y=$\frac{7}{8}$a时,才能使粒子击中PQ时的位置离P最远,最远距离为$\frac{9}{4}$a.
点评 带电粒子在磁场中运动的题目解题步骤为:定圆心、画轨迹、求半径.要掌握左手定则,熟练运用牛顿第二定律研究半径.


| A. | a光的折射率大 | B. | b光的折射率大 | ||
| C. | a光在三棱镜中的速度大 | D. | b光在三棱镜中的速度大 |

| A. | 大小为$\overline{OC}$,方向向左 | B. | 大小为$\overline{OC}$,方向向右 | ||
| C. | 大小为$\overline{AC}$,方向向左 | D. | 大小为$\overline{AC}$,方向向右 |
| A. | 恒星的质量为$\frac{{V}^{3}T}{2πG}$ | B. | 行星运动的轨道半径$\frac{VT}{2πG}$ | ||
| C. | 行星的质量为$\frac{2{π}^{2}{V}^{3}}{G{T}^{2}}$ | D. | 行星运动的加速度为$\frac{2πV}{GT}$ |
 如图所示,在边长为a的三角形区域内有匀强磁场,磁感应强度为B,其方向垂直纸面向里.一个边长也为a的等边三角形导线框ABC正好与上述磁场区域的边界重合.现使导线框以角速度ω绕其中心O点在纸面内匀速转动,当转过$\frac{π}{3}$时,导线框的转到图中虚线位置,已知导线框的总电阻为R,则在这段时间内 ( )
如图所示,在边长为a的三角形区域内有匀强磁场,磁感应强度为B,其方向垂直纸面向里.一个边长也为a的等边三角形导线框ABC正好与上述磁场区域的边界重合.现使导线框以角速度ω绕其中心O点在纸面内匀速转动,当转过$\frac{π}{3}$时,导线框的转到图中虚线位置,已知导线框的总电阻为R,则在这段时间内 ( )| A. | 因不知顺时针转动还是逆时针转动,所以不能判断导线框中的感应电流方向 | |
| B. | 导线框中感应电流方向为A→B→C | |
| C. | 能过导线框中任一截面的电量为$\frac{\sqrt{3}B{a}^{2}}{12R}$ | |
| D. | 导线框中平均感应电动势大小等于$\frac{\sqrt{3}B{a}^{2}ω}{4πR}$ |
 用如下的器材和方法可以验证“力的平行四边形定则”.在圆形桌子桌面平铺一张白纸,在桌子边缘安装三个光滑的滑轮,其中,滑轮P1固定在桌子边,滑轮P2、P3可沿桌边移动.第一次实验中,步骤如下:
用如下的器材和方法可以验证“力的平行四边形定则”.在圆形桌子桌面平铺一张白纸,在桌子边缘安装三个光滑的滑轮,其中,滑轮P1固定在桌子边,滑轮P2、P3可沿桌边移动.第一次实验中,步骤如下: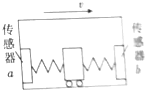 在矩形箱子的前、后壁上各装一个压力传感器,再用两根相同的轻弹簧夹着一个可无摩擦滑动的质量为1.0kg的滑块,两弹簧的另一端分别压在传感器a、b上,其压力大小可直接由传感器读出,如图所示.此装置可以测量汽车的加速度.现将它沿运动方向固定在汽车上,传感器b在前,传感器a在后.已知汽车静止时,传感器a、b的示数均为10N,取g=10m/s2.
在矩形箱子的前、后壁上各装一个压力传感器,再用两根相同的轻弹簧夹着一个可无摩擦滑动的质量为1.0kg的滑块,两弹簧的另一端分别压在传感器a、b上,其压力大小可直接由传感器读出,如图所示.此装置可以测量汽车的加速度.现将它沿运动方向固定在汽车上,传感器b在前,传感器a在后.已知汽车静止时,传感器a、b的示数均为10N,取g=10m/s2. 湖南方言中的“逗霸”来源于“斗把”,其本意是给锤子、铁锹等安装木制手柄的过程,下面将这一过程简化为如下的物理模型,如图所示,一高度可以忽略的圆环形铁锤套在粗细均匀的圆柱形木柄上,铁锤到手柄下端长l=50.0cm.为了使铁锤安装到手柄下端,先用手抓住手柄上端,使手柄与铁锤由静止开始一起竖直向下做匀加速直线运动,t=0.40s时,手柄下端碰到地面立即停止运动,此时手柄下降高度H=1.2m,铁锤恰能安装到手柄的下端.设铁锤相对手柄滑动时受到的摩擦力恒定,不计空气阻力,重力加速度g=10m/s2.求:
湖南方言中的“逗霸”来源于“斗把”,其本意是给锤子、铁锹等安装木制手柄的过程,下面将这一过程简化为如下的物理模型,如图所示,一高度可以忽略的圆环形铁锤套在粗细均匀的圆柱形木柄上,铁锤到手柄下端长l=50.0cm.为了使铁锤安装到手柄下端,先用手抓住手柄上端,使手柄与铁锤由静止开始一起竖直向下做匀加速直线运动,t=0.40s时,手柄下端碰到地面立即停止运动,此时手柄下降高度H=1.2m,铁锤恰能安装到手柄的下端.设铁锤相对手柄滑动时受到的摩擦力恒定,不计空气阻力,重力加速度g=10m/s2.求: 滑雪是人们喜爱的运动项目,当滑雪板的速度比较大时,在滑雪板与雪地间形成一个暂时的“气垫”,从而减小雪地与滑雪板间的动摩擦因数,然而当滑雪板相对雪地速度较小时,滑雪板就会陷入雪地中,使得它们间的动摩擦因数增大.设滑雪者的速度超过v0=4m/s时,滑雪板与雪地间的动摩擦因数就会由μ1=0.25变为μ2=0.1.一滑雪者从某一坡顶滑下,滑到坡底A的速度VA=25m/s,经过一段长为92m的水平雪地后,又刚好滑到另一倾角为37°的小山坡BC点的C点(B处有一光滑小圆弧连接),如图所示,不计空气阻力,g取=10m/s2,sin37°=0.6,cos37°=0.8,求:
滑雪是人们喜爱的运动项目,当滑雪板的速度比较大时,在滑雪板与雪地间形成一个暂时的“气垫”,从而减小雪地与滑雪板间的动摩擦因数,然而当滑雪板相对雪地速度较小时,滑雪板就会陷入雪地中,使得它们间的动摩擦因数增大.设滑雪者的速度超过v0=4m/s时,滑雪板与雪地间的动摩擦因数就会由μ1=0.25变为μ2=0.1.一滑雪者从某一坡顶滑下,滑到坡底A的速度VA=25m/s,经过一段长为92m的水平雪地后,又刚好滑到另一倾角为37°的小山坡BC点的C点(B处有一光滑小圆弧连接),如图所示,不计空气阻力,g取=10m/s2,sin37°=0.6,cos37°=0.8,求: