题目内容
18.图甲为竖直放置的离心轨道,其中圆轨道的半径r=0.50m,在轨道的最低点A和最高点B各安装了一个压力传感器(图中未画出),小球(可视为质点)从斜轨道的不同高度由静止释放,可测出小球在轨道内侧通过这两点时对轨道的压力FA和FB.g取10m/s2.
(1)若不计小球所受阻力,且小球恰能过B点,求小球通过A点时速度vA的大小;
(2)若不计小球所受阻力,小球每次都能通过B点,FB随FA变化的图线如图乙中的a所示,求小球的质量m;
(3)若小球所受阻力不可忽略,小球的质量m=0.15kg,FB随FA变化的图象如图乙中的b所示,求当FA=16N时,小球从A运动到B的过程中损失的机械能△E.
分析 (1)小球滚到两圆轨道最高点时恰能过B点,此时对轨道无压力,仅受重力,运用向心力公式可求出在其位置的速度.对于从A到B过程,根据机械能守恒定律,可求A点速度
(2)由图象可知,小球恰能过B点时,对A点压力为6N,根据牛顿运动定律可求此时的重力
(3)根据图乙可知:当小球通过B点时,若小球对轨道压力的大小FB=6.0N,则小球通过A点时对轨道压力的大小FA=16N,由牛顿第二定律可得此两位置的速度,进而求得机械能的损失
解答 解:(1)若小球恰能通过B点,设此时小球质量为m,通过B时的速度为vB.
根据牛顿第二定律有:mg=m$\frac{{v}_{B}^{2}}{r}$,
根据机械能守恒定律有:$\frac{1}{2}$mvA2=$\frac{1}{2}$mvB2+mg•2r,
代入数据解得:vA≈2.2m/s;
(2)根据第(1)问及图乙可知:当小球通过A点时的速度为2.2m/s时,小球对轨道压力的大小FA1=6N.设小球通过A点时,轨道对小球支持力的大小为FA2.
根据牛顿运动定律有:FA1=FA2,且有:FA2-mg=m$\frac{{v}_{A}^{2}}{r}$,
代入数据解得:m=0.1kg;
(3)根据图乙可知:当小球通过B点时,若小球对轨道压力的大小FB=6.0N,
则小球通过A点时对轨道压力的大小FA=16N.
设轨道对小球通过A、B时支持力的大小分别为FA′、FB′,速度分别为vA′、vB′,
根据牛顿运动定律有:FA′=FA,FA′-mg=m$\frac{v{′}_{A}^{2}}{r}$,FB=FB′,FB′+mg=m$\frac{v{′}_{B}^{2}}{r}$,
在小球从A运动到C的过程中,根据功能原理又有:$\frac{1}{2}$mvA′2=$\frac{1}{2}$mvB′2+mg•2r+△E,
代入数据解得:△E=0.2J;
答:(1)若不计小球所受阻力,且小球恰能过B点,求小球通过A点时速度的大小为2.2m/s;
(2)若不计小球所受阻力,小球每次都能通过B点,FB随FA变化的图线如图乙中的a所示,小球的质量0.1kg;
(3)小球从A运动到B的过程中损失的机械能0.2J.
点评 知道“小球恰能过B点”的含义,能够读懂图象隐含的信息,是解决本题的关键.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案| A. | 天然放射现象揭示了原子是可以再分的 | |
| B. | 某放射性元素的原子核发生了一次a衰变,则其质子数减小2 | |
| C. | β射线为原子的核外电子电离后形成的电子流 | |
| D. | 氢原子从高能级向低能级跃迁的过程中会辐射一定频率的光子 |

| A. | 甲的情况 | B. | 乙的情况 | C. | 丙的情况 | D. | 丁的情况 |
| A. | 0V | B. | 约0.8V | C. | 12V | D. | 120V |
| A. | 微波宜用地波传播 | |
| B. | 无线电选台的过程就是调制 | |
| C. | 在广播电视中,声音和图象信号可以利用电磁波传递 | |
| D. | 真空中电磁波的传播速度对不同惯性参考系是不同的 |




 如图所示的空间分布Ⅰ、Ⅱ、Ⅲ三个区域,各边界面相互平行,Ⅰ区域是电压为U的平行板电场,Ⅱ、Ⅲ区域为匀强磁场,磁场的方向分别为垂直纸面向外和垂直纸面向里,磁感应强度大小分别为B和2B,两个磁场区域宽度均为d,一质量为m、电荷量为q的正粒子从O1点由静止释放,通过N板小孔O2后水平垂直进入磁场区域Ⅱ,已知粒子的荷质比满足关系:$\frac{q}{m}$=$\frac{U}{2{d}^{2}{B}^{2}}$,粒子的重力忽略不计.求:
如图所示的空间分布Ⅰ、Ⅱ、Ⅲ三个区域,各边界面相互平行,Ⅰ区域是电压为U的平行板电场,Ⅱ、Ⅲ区域为匀强磁场,磁场的方向分别为垂直纸面向外和垂直纸面向里,磁感应强度大小分别为B和2B,两个磁场区域宽度均为d,一质量为m、电荷量为q的正粒子从O1点由静止释放,通过N板小孔O2后水平垂直进入磁场区域Ⅱ,已知粒子的荷质比满足关系:$\frac{q}{m}$=$\frac{U}{2{d}^{2}{B}^{2}}$,粒子的重力忽略不计.求: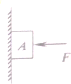 如图 6--4所示,在F作用下,质量为10kg的物体A静止在竖直墙上,这时F=50N,如果F增大为100N,A还静止在墙上,在这两种情况下,A所受到的摩擦力如何变化?(g取10m/s2)
如图 6--4所示,在F作用下,质量为10kg的物体A静止在竖直墙上,这时F=50N,如果F增大为100N,A还静止在墙上,在这两种情况下,A所受到的摩擦力如何变化?(g取10m/s2)