题目内容
1. 发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3,轨道1、2相切于Q点,轨道2、3相切于P点,如图所示.则在卫星分别在1、2、3轨道上正常运行时,以下说法正确的是( )
发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3,轨道1、2相切于Q点,轨道2、3相切于P点,如图所示.则在卫星分别在1、2、3轨道上正常运行时,以下说法正确的是( )| A. | 卫星在轨道3上的角速度小于在轨道1上的角速度 | |
| B. | 卫星在轨道3上的速率大于在轨道1上的速率 | |
| C. | 卫星在轨道2上经过P点时的速度小于它在轨道3上经过P点时的速度 | |
| D. | 卫星在轨道2上经过P点时的加速度等于它在轨道3上经过P点时的加速度 |
分析 根据人造卫星的万有引力等于向心力,列式求出线速度、角速度、和向心力的表达式进行讨论即可
卫星做逐渐远离圆心的运动,要实现这个运动必须使卫星所需向心力大于万有引力,所以应给卫星加速.
解答 解:A、卫星绕中心天体做匀速圆周运动,由万有引力提供向心力,
$\frac{GMm}{{r}^{2}}$=$\frac{{m4π}^{2}r}{{T}^{2}}$
T=2$π\sqrt{\frac{{\;r}^{3}}{GM}}$,
轨道3半径比轨道1半径大,所以卫星在轨道3上的周期大于在轨道1上的周期,
根据公式:$T=\frac{2π}{ω}$
所以:ω=$\sqrt{\frac{GM}{{r}^{3}}}$,所以卫星在轨道3上的角速度小于在轨道1上的角速度.故A正确;
B、根据万有引力提供向心力得:
$\frac{GMm}{{r}^{2}}$=$\frac{m{v}^{2}}{r}$
所以v=$\sqrt{\frac{GM}{r}}$
所以卫星在轨道3上的速率小于在轨道1上的速率.故B错误;
C、从轨道2到轨道3,卫星在P点是从做靠近圆心的运动到做匀速圆周运动,要实现这个运动必须使卫星所需向心力增大,所以应给卫星加速,增加所需的向心力.所以在轨道2上P点的速度小于轨道3上P点的速度,故C正确;
D、卫星运行时只受万有引力,加速度a=$\frac{GM}{{r}^{2\;}}$,所以卫星在轨道2上经过P点时的加速度等于它在轨道3上经过P点时的加速度,故D正确;
故选:ACD
点评 本题关键抓住万有引力提供向心力,先列式求解出线速度和角速度的表达式,再进行讨论.知道知道卫星变轨的原理,卫星通过加速或减速来改变所需向心力实现轨道的变换.

练习册系列答案
相关题目
11.如图所示是一定质量的理想气体的状态变化图线,下列说法正确的是( )
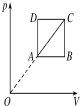

| A. | 由状态A变化到状态B,气体分子的平均动能增大 | |
| B. | 由状态A变化到状态C,气体内能不变 | |
| C. | 由A经B到C的过程与由A经D到C的过程,气体对外做功相同 | |
| D. | 由A经B到C、由A经D到C、由A直接到C的三个过程中,气体均吸热,但是吸热量不同 |
9.甲、乙两辆汽车均以相同速率向东行驶,关于参考系,下列说法中错误的是( )
| A. | 若以甲为参考系,乙是静止的 | |
| B. | 如观察结果是两辆车均静止,参考系可以是第三辆车 | |
| C. | 如以在甲车中一个走动的人为参考系,乙车仍是静止的 | |
| D. | 如甲车突然刹车停下,以乙车为参考系,甲车往西行驶 |
16.以v0的速度水平抛出一物体,当其竖直分速度大小与水平分速度大小相等时,此物体的( )
| A. | 水平分位移的大小等于竖直分位移大小的两倍 | |
| B. | 即时速率为$\sqrt{5}{v_0}$ | |
| C. | 运动时间为$\frac{2{v}_{0}}{g}$ | |
| D. | 运动的位移是$\frac{\sqrt{2}{v}_{0}^{2}}{2g}$ |
 滑板运动是一种陆地上的“冲浪运动”,滑板运动员可在不同的滑坡上滑行,做出各种动作,给人以美的享受.如图是模拟的滑板组合滑行轨道,该轨道由足够长的斜直轨道、半径R1=1m的凹形圆弧轨道和半径R2=1.6m的凸形圆弧轨道组成,这三部分轨道处于同一竖直平面内且依次平滑连接,其中M点为凹形圆弧轨道的最低点,N点为凸形圆弧轨道的最高点,凸形圆弧轨道的圆心O点与M点处在同一水平面上,一质量为m=1kg可看作质点的滑板,从斜直轨道上的P点无初速滑下,经过M点滑向N点,P点距M点所在水平面的高度h=1.8m,不计一切阻力,g取10m/s2.
滑板运动是一种陆地上的“冲浪运动”,滑板运动员可在不同的滑坡上滑行,做出各种动作,给人以美的享受.如图是模拟的滑板组合滑行轨道,该轨道由足够长的斜直轨道、半径R1=1m的凹形圆弧轨道和半径R2=1.6m的凸形圆弧轨道组成,这三部分轨道处于同一竖直平面内且依次平滑连接,其中M点为凹形圆弧轨道的最低点,N点为凸形圆弧轨道的最高点,凸形圆弧轨道的圆心O点与M点处在同一水平面上,一质量为m=1kg可看作质点的滑板,从斜直轨道上的P点无初速滑下,经过M点滑向N点,P点距M点所在水平面的高度h=1.8m,不计一切阻力,g取10m/s2.