题目内容
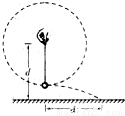
小明站在水平地面上,手握不可伸长的轻绳一端,绳的另一端系有质量为m的小球,甩动手腕,使球在竖直平面内做圆周运动.当球某次运动到最低点时,绳突然断掉,球飞行水,平距离d后落地,如图所示,已知握绳的手离地面高度为d,手与球之间的绳长为
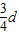 ,重力加速度为g.忽略手的运动半径和空气阻力.求:
,重力加速度为g.忽略手的运动半径和空气阻力.求:(1)绳断时球的速度大小v1;
(2)绳能承受的最大拉力;
(3)改变绳长(绳承受的最大拉力不变),保持手的位置不动,使球重复上述运动,若绳仍在球运动到最低点时断掉,要使球抛出的水平距离最大,绳长应为多少?最大水平距离为多少?
【答案】分析:(1)绳断后,小球做平抛运动,根据平抛运动的高度求出时间,根据水平位移和时间求出绳断时球的速度大小.
(2)根据在最低点,合力提供向心力,运用牛顿第二定律求出最大拉力.
(3)根据最大拉力,通过牛顿第二定律求出绳断后的速度与绳长的关系,根据平抛运动求出平抛运动水平位移的表达式,通过数学方法二次函数求极值,求出l为多少时,x最大.
解答:解:(1)设绳断后球做平抛运动的时间为t1,
竖直方向上: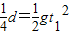 ,水平方向上:d=v1t1
,水平方向上:d=v1t1
解得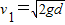 .
.
(2)设绳能承受的最大拉力为Fm.
球做圆周运动的半径为R=
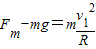
解得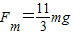 .
.
(3)设绳长为l,绳断时球的速度为v2.
有: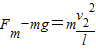 ,解得
,解得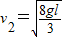 .
.
绳断后球做平抛运动,竖直位移为d-l,水平位移为x,时间为t2.
有: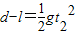 ,x=v2t2.
,x=v2t2.
得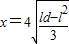
当l=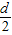 时,x有极大值
时,x有极大值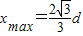 .
.
答:(1)绳断时球的速度大小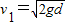 .
.
(2)绳能承受的最大拉力为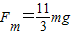 .
.
(3)要使球抛出的水平距离最大,绳长应为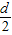 ,最大水平距离为
,最大水平距离为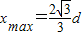 .
.
点评:本题综合了平抛运动和圆周运动两个运动,关键知道平抛运动在竖直方向和水平方向上的运动规律,以及圆周运动向心力的来源.
(2)根据在最低点,合力提供向心力,运用牛顿第二定律求出最大拉力.
(3)根据最大拉力,通过牛顿第二定律求出绳断后的速度与绳长的关系,根据平抛运动求出平抛运动水平位移的表达式,通过数学方法二次函数求极值,求出l为多少时,x最大.
解答:解:(1)设绳断后球做平抛运动的时间为t1,
竖直方向上:
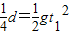 ,水平方向上:d=v1t1
,水平方向上:d=v1t1解得
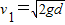 .
.(2)设绳能承受的最大拉力为Fm.
球做圆周运动的半径为R=

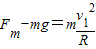
解得
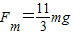 .
.(3)设绳长为l,绳断时球的速度为v2.
有:
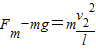 ,解得
,解得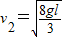 .
.绳断后球做平抛运动,竖直位移为d-l,水平位移为x,时间为t2.
有:
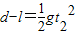 ,x=v2t2.
,x=v2t2.得
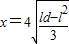
当l=
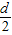 时,x有极大值
时,x有极大值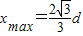 .
.答:(1)绳断时球的速度大小
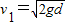 .
.(2)绳能承受的最大拉力为
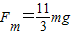 .
.(3)要使球抛出的水平距离最大,绳长应为
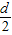 ,最大水平距离为
,最大水平距离为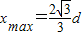 .
.点评:本题综合了平抛运动和圆周运动两个运动,关键知道平抛运动在竖直方向和水平方向上的运动规律,以及圆周运动向心力的来源.

练习册系列答案
相关题目
 (2011?无锡一模)小明站在水平地面上,手握不可伸长的轻绳一端,绳的另一端系有质量为m的小球,甩动手腕,使球在竖直平面内做圆周运动.当球某次运动到最低点时,绳突然断掉,球飞行水平距离d后落地.如题图所示.已知握绳的手离地面高度为d,手与球之间的绳长为
(2011?无锡一模)小明站在水平地面上,手握不可伸长的轻绳一端,绳的另一端系有质量为m的小球,甩动手腕,使球在竖直平面内做圆周运动.当球某次运动到最低点时,绳突然断掉,球飞行水平距离d后落地.如题图所示.已知握绳的手离地面高度为d,手与球之间的绳长为 小明站在水平地面上,手握不可伸长的轻绳一端,绳的另一端系有质量为m的小球,甩动手腕,使球在竖直平面内做圆周运动.当球某次运动到最低点时,绳突然断掉,球飞行水,
小明站在水平地面上,手握不可伸长的轻绳一端,绳的另一端系有质量为m的小球,甩动手腕,使球在竖直平面内做圆周运动.当球某次运动到最低点时,绳突然断掉,球飞行水, 小明站在水平地面上,手握不可伸长的轻绳一端,绳的另一端系有质量为m的小球,甩动手腕,使球在竖直平面内做圆周运动.当球某次运动到最低点时,绳恰好断掉,球飞行水平距离d后落地.如图所示.已知握绳的手离地面高度为d,手与球之间的绳长为
小明站在水平地面上,手握不可伸长的轻绳一端,绳的另一端系有质量为m的小球,甩动手腕,使球在竖直平面内做圆周运动.当球某次运动到最低点时,绳恰好断掉,球飞行水平距离d后落地.如图所示.已知握绳的手离地面高度为d,手与球之间的绳长为 小明站在水平地面上,手握不可伸长的轻绳一端,绳的另一端系有质量为m的小球,甩动手腕,使球在竖直平面内做圆周运动。当球某次运动到最低点时,绳突然断掉,球飞行水平距离d后落地。如题24图所示。已知握绳的手离地面高度为d,手与球之间的绳长为
小明站在水平地面上,手握不可伸长的轻绳一端,绳的另一端系有质量为m的小球,甩动手腕,使球在竖直平面内做圆周运动。当球某次运动到最低点时,绳突然断掉,球飞行水平距离d后落地。如题24图所示。已知握绳的手离地面高度为d,手与球之间的绳长为