题目内容

一个质量为0.06kg的弹性小球，在光滑水平面上以8m/s的速度垂直撞到墙上，碰撞后小球沿相反方向运动，反弹后的速度大小与碰撞前相同．则碰撞前后小球速度变化量的大小△υ和碰撞过程中墙对小球做功的大小W为（　　）
分析：速度是矢量，速度的变化量应该采用平行四边形法则求解．对于同一直线上的速度变化量的求解，我们可以运用表达式△v=v2-v1，但必须规定正方向．
运用动能定理求出碰撞过程中墙对小球做功．
解答：解：A、B规定初速度方向为正方向，初速度为：v1=8m/s，碰撞后速度为：v2=-8m/s；
△v=v2-v1=-8-8=-16m/s，负号表示速度变化量的方向与初速度方向相反；故A错误．B正确．
C、D运用动能定理研究碰撞过程，由于初、末动能相等，动能的变化量为0，所以W=△Ek=0．所以，碰撞过程中墙对小球做功的大小W为0．故C正确．故D错误．
故选：BC
点评：对于矢量的运算要根据平行四边形法则，关键要考虑矢量的方向，动能定理是一个标量等式，对于动能定理的研究，则无需考虑方向．
练习册系列答案
相关题目
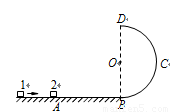
如图所示，水平光滑轨道AB与以O点为圆心的竖直半圆形光滑轨道BCD相切于B点，半圆形轨道的半径r=0.30m．在水平轨道上A点静置一质量为m2=0.12kg的物块2，现有一个质量m1=0.06kg的物块1以一定的速度向物块2运动，并与之发生正碰，碰撞过程中无机械能损失，碰撞后物块2的速度v2=4.0m/s．物块均可视为质点，g取10m/s2，求：
（1）物块2运动到B点时对半圆形轨道的压力大小；
（2）发生碰撞前物块1的速度大小；
（3）若半圆形轨道的半径大小可调，则在题设条件下，为使物块2能通过半圆形轨道的最高点，其半径大小应满足什么条件．
如图甲，PNQ为竖直放置的半径为0.1m的半圆形轨道，在轨道的最低点P和最高点Q各安装了一个压力传感器，可测定小球在轨道内侧，通过这两点时对轨道的压力FP和FQ．轨道的下端与一光滑水平轨道相切，水平轨道上有一质量为0.06kg的小球A，以不同的初速度v0与静止在轨道最低点P处稍右侧的另一质量为0.04kg的小球B发生碰撞，碰后精英家教网形成一整体（记为小球C）以共同速度v冲入PNQ轨道．（A、B、C三小球均可视为质点，g取10m/s2）
（1）若FP和FQ的关系图线如图乙所示，求：当 FP=13N 时所对应的入射小球A的初速度v0为多大？
（2）当FP=13N时，AB所组成的系统从A球开始向左运动到整体达到轨道最高点Q全过程中所损失的总机械能为多少？
（3）若轨道PNQ光滑，小球C均能通过Q点．试推导FP随FQ变化的关系式，并在图丙中画出其图线．

如图所示，水平光滑轨道AB与以O点为圆心的竖直半圆形光滑轨道BCD相切于B点，半圆形轨道的半径r=0.30m。在水平轨道上A点静置一质量为m2=0.12kg的物块2，现有一个质量m1=0.06kg的物块1以一定的速度向物块2运动，并与之发生正碰，碰撞过程中无机械能损失，碰撞后物块2的速度v2=4.0m/s。物块均可视为质点，g取10m/s2，求：

1.物块2运动到B点时对半圆形轨道的压力大小；

2.发生碰撞前物块1的速度大小；

3.若半圆形轨道的半径大小可调，则在题设条件下，为使物块2能通过半圆形轨道的最高点，其半径大小应满足什么条件。

 

 

如图所示，水平光滑轨道AB与以O点为圆心的竖直半圆形光滑轨道BCD相切于B点，半圆形轨道的半径r=0.30m。在水平轨道上A点静置一质量为m2=0.12kg的物块2，现有一个质量m1=0.06kg的物块1以一定的速度向物块2运动，并与之发生正碰，碰撞过程中无机械能损失，碰撞后物块2的速度v2=4.0m/s。物块均可视为质点，g取10m/s2，求：

1.物块2运动到B点时对半圆形轨道的压力大小；

2.发生碰撞前物块1的速度大小；

3.若半圆形轨道的半径大小可调，则在题设条件下，为使物块2能通过半圆形轨道的最高点，其半径大小应满足什么条件。

 

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网