题目内容
如图所示,在xoy平面直角坐标系第一象限内分布有垂直向外的匀强磁场,磁感应强度大小B=2.5×10-2T,在第二象限紧贴y轴和x轴放置一对平行金属板MN(中心轴线过y轴),极板间距d=0.4m,极板与左侧电路相连接。通过移动滑动头P可以改变极板MN间的电压。a、b为滑动变阻器的最下端和最上端(滑动变阻器的阻值分布均匀),a、b两端所加电压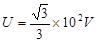 。在MN中心轴线上距y轴距离为L=0.4m处有一粒子源S,沿x轴正方向连续射出比荷为
。在MN中心轴线上距y轴距离为L=0.4m处有一粒子源S,沿x轴正方向连续射出比荷为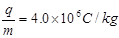 ,速度为vo=2.0×104m/s带正电的粒子,粒子经过y轴进入磁场后从x轴射出磁场(忽略粒子的重力和粒子之间的相互作用)。
,速度为vo=2.0×104m/s带正电的粒子,粒子经过y轴进入磁场后从x轴射出磁场(忽略粒子的重力和粒子之间的相互作用)。
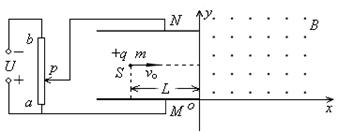
(1)当滑动头P在ab正中间时,求粒子射入磁场时速度的大小。
(2)当滑动头P在ab间某位置时,粒子射出极板的速度偏转角为 ,试写出粒子在磁场中运动的时间与
,试写出粒子在磁场中运动的时间与 的函数关系,并由此计算粒子在磁场中运动的最长时间。
的函数关系,并由此计算粒子在磁场中运动的最长时间。
(1)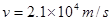 (2)
(2)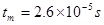
【解析】(1)当滑动头P在ab正中间时,极板间电压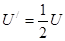 ,粒子在电场中做类平抛运动,设粒子射入磁场时沿y轴方向的分速度为
,粒子在电场中做类平抛运动,设粒子射入磁场时沿y轴方向的分速度为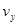 :
:
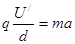 ①
①
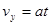 ②
②
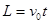 ③
③
粒子射入磁场时速度的大小设为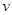
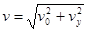 ④
④
解得: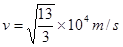 (或
(或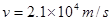 )
⑤
)
⑤
(2)当滑动头P在a端时,粒子在磁场中运动的速度大小为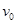 ,有
,有
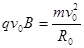 ⑥
⑥
解得: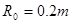 ⑦
⑦
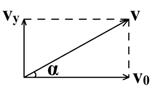
设粒子射出极板时速度的大小为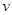 ,偏向角为α,在磁场中圆周运动半径为
,偏向角为α,在磁场中圆周运动半径为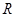 。根据速度平行四边形可得:
。根据速度平行四边形可得:
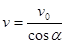 ⑧
⑧
由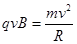 可得:
可得: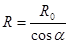 ⑨
⑨
粒子在磁场中做圆周运动的轨迹如图所示,圆心为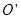 ,与x轴交点为D,
,与x轴交点为D,
设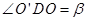 ,根据几何关系:
,根据几何关系:
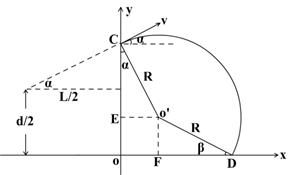
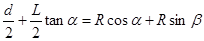 ⑩
⑩
又: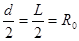
解得: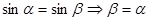 11
11
粒子在磁场中运动的周期为T:
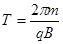 12
12
则粒子在磁场中运动的时间:
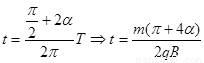 13
13
由此结果可知,粒子射入磁场时速度偏转角越大则粒子在磁场中运动的时间就越大。假设极板间电压为最大值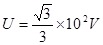 时粒子能射出电场,则此粒子在磁场中运动的时间最长。
时粒子能射出电场,则此粒子在磁场中运动的时间最长。
由(1)问规律可知当滑动头P在b端时,粒子射入磁场时沿y方向的分速度:
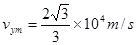 14
14
y方向偏距: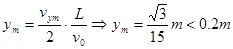 ,说明粒子可以射出极板。
15
,说明粒子可以射出极板。
15
此时粒子速度偏转角最大,设为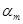 ,
,
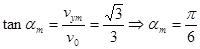 16
16
故粒子在磁场中运动的最长时间:
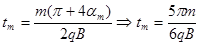 17
17
代入数值得: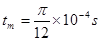 (或
(或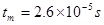 ) 18
) 18
注:当电压最大为U时粒子能从极板间射出需要说明,若没有说明(或证明)扣2分。
评分标准:本题19分. (1)问6分,①、②、③、④式各1分,⑤式2分;(2)问13分,⑥—11式共5分,12、13式共2分,14、15式共2分,16、17、18式共4分。
本题考查了粒子在电磁场中的运动,粒子现在电场中作类平抛运动,然后进入磁场,做圆周运动,类平抛运动可将其分解为水平方向和竖直方向两个运动,利用分运动的同时性特点进行解题,现根据计算算出粒子在磁场中的运动时间表达式可得出粒子射入磁场时速度偏转角越大则粒子在磁场中运动的时间就越大,从而解出。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 (2013?安徽模拟)如图所示,在xoy平面上,直线OM与x轴正方向夹角为45°,直线OM左侧存在平行y轴的匀强电场,方向沿y轴负方向.直线OM右侧存在垂直xoy平面向里的磁感应强度为B的匀强磁场.一带电量为q质量为m带正电的粒子(忽略重力)从原点O沿x轴正方向以速度vo射入磁场.此后,粒子穿过磁场与电场的边界三次,恰好从电场中回到原点O.(粒子通过边界时,其运动不受边界的影响)试求:
(2013?安徽模拟)如图所示,在xoy平面上,直线OM与x轴正方向夹角为45°,直线OM左侧存在平行y轴的匀强电场,方向沿y轴负方向.直线OM右侧存在垂直xoy平面向里的磁感应强度为B的匀强磁场.一带电量为q质量为m带正电的粒子(忽略重力)从原点O沿x轴正方向以速度vo射入磁场.此后,粒子穿过磁场与电场的边界三次,恰好从电场中回到原点O.(粒子通过边界时,其运动不受边界的影响)试求: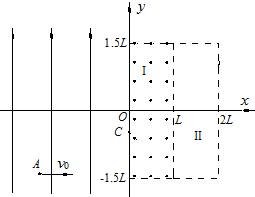 如图所示,在xOy平面的y轴左侧存在沿y轴正方向的匀强电场,y轴右侧区域Ⅰ内存在磁感应强度大小B1=
如图所示,在xOy平面的y轴左侧存在沿y轴正方向的匀强电场,y轴右侧区域Ⅰ内存在磁感应强度大小B1= (2006?连云港二模)如图所示,在xoy平面上,一个以原点O为中心、半径为R的圆形区域内存在着一匀强磁场.磁场的磁感应强度为B,方向垂直于xoy平面向里.在O点处原来静止着一个具有放射性的原子核--氮(
(2006?连云港二模)如图所示,在xoy平面上,一个以原点O为中心、半径为R的圆形区域内存在着一匀强磁场.磁场的磁感应强度为B,方向垂直于xoy平面向里.在O点处原来静止着一个具有放射性的原子核--氮( 如图所示,在xOy平面上,一个以原点O为圆心,半径为4R的原型磁场区域内存在着匀强磁场,磁场的方向垂直于纸面向里,在坐标(-2R,0)的A处静止着一个具有放射性的原子核氮713N.某时刻该核发生衰变,放出一个正电子和一个反冲核,已知正电子从A处射出时速度方向垂直于x轴,且后来通过了y轴,而反冲核刚好不离开磁场区域.不计重力影响和离子间的相互作用.
如图所示,在xOy平面上,一个以原点O为圆心,半径为4R的原型磁场区域内存在着匀强磁场,磁场的方向垂直于纸面向里,在坐标(-2R,0)的A处静止着一个具有放射性的原子核氮713N.某时刻该核发生衰变,放出一个正电子和一个反冲核,已知正电子从A处射出时速度方向垂直于x轴,且后来通过了y轴,而反冲核刚好不离开磁场区域.不计重力影响和离子间的相互作用.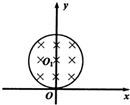 如图所示,在xOy平面上,以y轴上点Ol为圆心,半径为R=0.3m的圆形区域内,分布着一个方向垂直于xOy平面向里,磁感应强度大小为B=0.5T的匀强磁场.一个比荷
如图所示,在xOy平面上,以y轴上点Ol为圆心,半径为R=0.3m的圆形区域内,分布着一个方向垂直于xOy平面向里,磁感应强度大小为B=0.5T的匀强磁场.一个比荷