题目内容
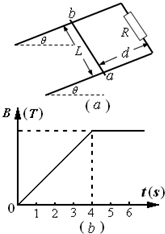 如图(a)所示,两根足够长、电阻不计的平行光滑金属导轨相距为L=1m,导轨平面与水平面成θ=30°角,上端连接R=1.5?的电阻;质量为m=0.2kg、阻值r=0.5?的金属棒ab放在两导轨上,距离导轨最上端为d=4m,棒与导轨垂直并保持良好接触.整个装置处于匀强磁场中,磁场方向与导轨平面垂直,磁感应强度大小随时间变化的情况如图(b)所示,前4s内为B=kt.前4s内,为保持ab棒静止,在棒上施加了一平行于导轨平面的外力F,已知当t=2s时,F恰好为零.求:
如图(a)所示,两根足够长、电阻不计的平行光滑金属导轨相距为L=1m,导轨平面与水平面成θ=30°角,上端连接R=1.5?的电阻;质量为m=0.2kg、阻值r=0.5?的金属棒ab放在两导轨上,距离导轨最上端为d=4m,棒与导轨垂直并保持良好接触.整个装置处于匀强磁场中,磁场方向与导轨平面垂直,磁感应强度大小随时间变化的情况如图(b)所示,前4s内为B=kt.前4s内,为保持ab棒静止,在棒上施加了一平行于导轨平面的外力F,已知当t=2s时,F恰好为零.求:(1)k;
(2)t=3s时,电阻R的热功率PR;
(3)前4s内,外力F随时间t的变化规律;
(4)从第4s末开始,外力F拉着导体棒ab以速度v沿斜面向下作匀速直线运动,且F的功率恒为P=6W,求v的大小.
分析:(1)在0~4s内,由法拉第电磁感应定律和闭合电路欧姆定律得到电流的表达式.根据ab棒静止,受力平衡,t=0时刻F=0,列式求k;
(2)结合上题的结果求出t=3s时电路中的电流I,由公式P=I2R求电阻R的热功率PR;
(3)根据F=BIL求出安培力,利用棒子的受力平衡求出外力F的大小和方向.
(4)根据从第4s末开始,外力F拉着导体棒ab以速度v沿斜面向下作匀速直线运动,合力为零,由P=Fv求外力F,由平衡条件列式,求v.
(2)结合上题的结果求出t=3s时电路中的电流I,由公式P=I2R求电阻R的热功率PR;
(3)根据F=BIL求出安培力,利用棒子的受力平衡求出外力F的大小和方向.
(4)根据从第4s末开始,外力F拉着导体棒ab以速度v沿斜面向下作匀速直线运动,合力为零,由P=Fv求外力F,由平衡条件列式,求v.
解答:解:(1)在0~4s内,由法拉第电磁感应定律得:
回路中产生的感应电动势为 ?=
=
Ld=kLd
感应电流为 I=
=
当t=2s时,F=0,由ab棒静止有
mgsinθ=ktIL=
∴k=
=
=0.5(T/s)
(2)前4s内,I=
=
=
A=1A
∴t=3s时,电阻R的热功率PR=I2R=12×1.5W=1.5W
(3)设沿斜面向上为F的正方向,则由ab棒受力平衡得
F+FA=mgsinθ
而 安培力 FA=BIL=ktIL
∴F=mgsinθ-kILt=(0.2×10×0.5-0.5×1×1t)N=(1-0.5t)N
(4)从第4s末开始,B=kt=2T,且不变,?=BLv,I=
=
则有
+mgsinθ=BIL
得:v=2m/s
答:
(1)k为0.5T/s;
(2)t=3s时,电阻R的热功率PR为1.5W.
(3)前4s内,外力F随时间t的变化规律是(1-0.5t)N;
(4)v的大小为2m/s.
回路中产生的感应电动势为 ?=
| △Φ |
| △t |
| △B |
| △t |
感应电流为 I=
| ? |
| R+r |
| kLd |
| R+r |
当t=2s时,F=0,由ab棒静止有
mgsinθ=ktIL=
| k2tL2d |
| R+r |
∴k=
|
|
(2)前4s内,I=
| ? |
| R+r |
| kLd |
| R+r |
| 0.5×1×4 |
| 1.5+0.5 |
∴t=3s时,电阻R的热功率PR=I2R=12×1.5W=1.5W
(3)设沿斜面向上为F的正方向,则由ab棒受力平衡得
F+FA=mgsinθ
而 安培力 FA=BIL=ktIL
∴F=mgsinθ-kILt=(0.2×10×0.5-0.5×1×1t)N=(1-0.5t)N
(4)从第4s末开始,B=kt=2T,且不变,?=BLv,I=
| ? |
| R+r |
| BLv |
| R+r |
则有
| p |
| v |
得:v=2m/s
答:
(1)k为0.5T/s;
(2)t=3s时,电阻R的热功率PR为1.5W.
(3)前4s内,外力F随时间t的变化规律是(1-0.5t)N;
(4)v的大小为2m/s.
点评:本题是电磁感应与力学知识、电路等知识的综合,解决本题的关键掌握法拉第电磁感应定律E=n
=n
S、导体棒切割产生的感应电动势E=BLv、安培力公式F=BIL和平衡条件.
| △φ |
| △t |
| △B |
| △t |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图(a)所示,两根足够长的光滑水平金属导轨相距为L=0.40m,导轨平面与水平面成θ=30°角,上端和下端通过导线分别连接阻值R1=R2=1.2Ω的电阻,质量为m=0.20kg、阻值r=0.20Ω的金属棒ab放在两导轨上,棒与导轨垂直并保持良好的接触,整个装置处在垂直导轨平面向上的匀强磁场中,磁感应强度大小为B=1T.现通过小电动机对金属棒施加拉力,使金属棒沿导轨向上做匀加速直线运动,0.5S时电动机达到额定功率,此后电动机功率保持不变,经足够长时间后,金属棒到达最大速度5.0m/S.此过程金属棒运动的v-t图象如图(b)所示,试求:(取重力加速度g=10m/s2)
如图(a)所示,两根足够长的光滑水平金属导轨相距为L=0.40m,导轨平面与水平面成θ=30°角,上端和下端通过导线分别连接阻值R1=R2=1.2Ω的电阻,质量为m=0.20kg、阻值r=0.20Ω的金属棒ab放在两导轨上,棒与导轨垂直并保持良好的接触,整个装置处在垂直导轨平面向上的匀强磁场中,磁感应强度大小为B=1T.现通过小电动机对金属棒施加拉力,使金属棒沿导轨向上做匀加速直线运动,0.5S时电动机达到额定功率,此后电动机功率保持不变,经足够长时间后,金属棒到达最大速度5.0m/S.此过程金属棒运动的v-t图象如图(b)所示,试求:(取重力加速度g=10m/s2)
 (2008?普陀区一模)如图(a)所示,两根足够长的水平平行金属导轨相距为L=0.5m,其右端通过导线连接阻值R=0.6Ω的电阻,导轨电阻不计,一根质量为m=0.2kg、阻值r=0.2Ω的金属棒ab放在两导轨上,棒与导轨垂直并保持良好接触,金属棒与导轨间的动摩擦因数μ=0.5.整个装置处在竖直向下的匀强磁场中,取g=10m/s2.若所加磁场的磁感应强度大小恒为B,通过小电动机对金属棒施加水平向左的牵引力,使金属棒沿导轨向左做匀加速直线运动,经过0.5s电动机的输出功率达到P=10W,此后电动机功率保持不变.金属棒运动的v~t图象如图(b)所示,试求:
(2008?普陀区一模)如图(a)所示,两根足够长的水平平行金属导轨相距为L=0.5m,其右端通过导线连接阻值R=0.6Ω的电阻,导轨电阻不计,一根质量为m=0.2kg、阻值r=0.2Ω的金属棒ab放在两导轨上,棒与导轨垂直并保持良好接触,金属棒与导轨间的动摩擦因数μ=0.5.整个装置处在竖直向下的匀强磁场中,取g=10m/s2.若所加磁场的磁感应强度大小恒为B,通过小电动机对金属棒施加水平向左的牵引力,使金属棒沿导轨向左做匀加速直线运动,经过0.5s电动机的输出功率达到P=10W,此后电动机功率保持不变.金属棒运动的v~t图象如图(b)所示,试求: (2008?东莞模拟)如图(a)所示,两根足够长的光滑平行金属导轨相距为L,导轨平面与水平面成θ角,上端通过导线连接阻值为R的电阻,阻值为r的金属棒ab放在两导轨上,棒与导轨垂直并保持良好接触,整个装置处在垂直导轨平面向上的磁场中,若所加磁场的磁感应强度大小恒为B,使金属棒沿导轨由静止向下运动,金属棒运动的v-t图象如图(b)所示,当t=t0时刻,物体下滑距离为s.已知重力加速度为g,导轨电阻忽略不计.试求:
(2008?东莞模拟)如图(a)所示,两根足够长的光滑平行金属导轨相距为L,导轨平面与水平面成θ角,上端通过导线连接阻值为R的电阻,阻值为r的金属棒ab放在两导轨上,棒与导轨垂直并保持良好接触,整个装置处在垂直导轨平面向上的磁场中,若所加磁场的磁感应强度大小恒为B,使金属棒沿导轨由静止向下运动,金属棒运动的v-t图象如图(b)所示,当t=t0时刻,物体下滑距离为s.已知重力加速度为g,导轨电阻忽略不计.试求: