题目内容
 如图(a)所示,两根足够长的光滑水平金属导轨相距为L=0.40m,导轨平面与水平面成θ=30°角,上端和下端通过导线分别连接阻值R1=R2=1.2Ω的电阻,质量为m=0.20kg、阻值r=0.20Ω的金属棒ab放在两导轨上,棒与导轨垂直并保持良好的接触,整个装置处在垂直导轨平面向上的匀强磁场中,磁感应强度大小为B=1T.现通过小电动机对金属棒施加拉力,使金属棒沿导轨向上做匀加速直线运动,0.5S时电动机达到额定功率,此后电动机功率保持不变,经足够长时间后,金属棒到达最大速度5.0m/S.此过程金属棒运动的v-t图象如图(b)所示,试求:(取重力加速度g=10m/s2)
如图(a)所示,两根足够长的光滑水平金属导轨相距为L=0.40m,导轨平面与水平面成θ=30°角,上端和下端通过导线分别连接阻值R1=R2=1.2Ω的电阻,质量为m=0.20kg、阻值r=0.20Ω的金属棒ab放在两导轨上,棒与导轨垂直并保持良好的接触,整个装置处在垂直导轨平面向上的匀强磁场中,磁感应强度大小为B=1T.现通过小电动机对金属棒施加拉力,使金属棒沿导轨向上做匀加速直线运动,0.5S时电动机达到额定功率,此后电动机功率保持不变,经足够长时间后,金属棒到达最大速度5.0m/S.此过程金属棒运动的v-t图象如图(b)所示,试求:(取重力加速度g=10m/s2)(1)电动机的额定功率P
(2)金属棒匀加速时的加速度a的大小
(3)在0~0.5s时间内电动机牵引力F与速度v的关系.
分析:(1)当棒匀速运动时,达到稳定状态,以恒定的速度运动,由于稳定时棒受力平衡,金属棒所受的合力为0,根据平衡条件和功率公式P=Fv得出此时棒所受的安培力F,即可求得P;
(2)在t时刻杆的速度为:v=at1,拉力此时的功率为:P=F1v,根据牛顿第二定律列式,可求得磁感应强度B;
(3)在0~0.5s时间内,金属棒做匀加速运动,由牛顿第二定律和安培力公式求电动机牵引力F与速度v的关系式.
(2)在t时刻杆的速度为:v=at1,拉力此时的功率为:P=F1v,根据牛顿第二定律列式,可求得磁感应强度B;
(3)在0~0.5s时间内,金属棒做匀加速运动,由牛顿第二定律和安培力公式求电动机牵引力F与速度v的关系式.
解答:解:(1)达到最大速度时P=F0vm
根据力的平衡有:F0-mgsinθ-F安=0;
外电路总电阻是:R并=
=0.6Ω
杆所受的安培力为:F安=
由图知:vm=5m/s,r=0.20Ω,m=0.2kg,r=0.20Ω,θ=30°,由以上几式解得P=10W
(2)金属棒匀加速时,在t1时刻杆的速度为:v=at1,拉力此时的功率为:P=F1v
根据牛顿第二定律有:F1-mgsinθ-
=ma;
由图t1=0.5s,m=0.2kg,R并=0.6Ω,r=0.20Ω,θ=30°,代入解得 a=
m/s2
(3)根据牛顿第二定律有F-mgsinθ-
=ma;
将m=0.2kg,R并=0.6Ω,r=0.20Ω,θ=30°代入解得 F=
+
.
答:
(1)电动机的额定功率P是20W.
(2)金属棒匀加速时的加速度a的大小是
m/s2.
(3)在0~0.5s时间内电动机牵引力F与速度v的关系是F=
+
.
根据力的平衡有:F0-mgsinθ-F安=0;
外电路总电阻是:R并=
| R1 |
| 2 |
杆所受的安培力为:F安=
| B2L2vm |
| R并+r |
由图知:vm=5m/s,r=0.20Ω,m=0.2kg,r=0.20Ω,θ=30°,由以上几式解得P=10W
(2)金属棒匀加速时,在t1时刻杆的速度为:v=at1,拉力此时的功率为:P=F1v
根据牛顿第二定律有:F1-mgsinθ-
| B2L2v |
| R并+r |
由图t1=0.5s,m=0.2kg,R并=0.6Ω,r=0.20Ω,θ=30°,代入解得 a=
| 20 |
| 3 |
(3)根据牛顿第二定律有F-mgsinθ-
| B2L2v |
| R并+r |
将m=0.2kg,R并=0.6Ω,r=0.20Ω,θ=30°代入解得 F=
| 7 |
| 3 |
| v |
| 5 |
答:
(1)电动机的额定功率P是20W.
(2)金属棒匀加速时的加速度a的大小是
| 20 |
| 3 |
(3)在0~0.5s时间内电动机牵引力F与速度v的关系是F=
| 7 |
| 3 |
| v |
| 5 |
点评:会正确分析导体棒受到的安培力的大小及计算式,熟悉功率的表达式,能分过程对导体棒的运动过程进行分析.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目

 (2008?普陀区一模)如图(a)所示,两根足够长的水平平行金属导轨相距为L=0.5m,其右端通过导线连接阻值R=0.6Ω的电阻,导轨电阻不计,一根质量为m=0.2kg、阻值r=0.2Ω的金属棒ab放在两导轨上,棒与导轨垂直并保持良好接触,金属棒与导轨间的动摩擦因数μ=0.5.整个装置处在竖直向下的匀强磁场中,取g=10m/s2.若所加磁场的磁感应强度大小恒为B,通过小电动机对金属棒施加水平向左的牵引力,使金属棒沿导轨向左做匀加速直线运动,经过0.5s电动机的输出功率达到P=10W,此后电动机功率保持不变.金属棒运动的v~t图象如图(b)所示,试求:
(2008?普陀区一模)如图(a)所示,两根足够长的水平平行金属导轨相距为L=0.5m,其右端通过导线连接阻值R=0.6Ω的电阻,导轨电阻不计,一根质量为m=0.2kg、阻值r=0.2Ω的金属棒ab放在两导轨上,棒与导轨垂直并保持良好接触,金属棒与导轨间的动摩擦因数μ=0.5.整个装置处在竖直向下的匀强磁场中,取g=10m/s2.若所加磁场的磁感应强度大小恒为B,通过小电动机对金属棒施加水平向左的牵引力,使金属棒沿导轨向左做匀加速直线运动,经过0.5s电动机的输出功率达到P=10W,此后电动机功率保持不变.金属棒运动的v~t图象如图(b)所示,试求: (2008?东莞模拟)如图(a)所示,两根足够长的光滑平行金属导轨相距为L,导轨平面与水平面成θ角,上端通过导线连接阻值为R的电阻,阻值为r的金属棒ab放在两导轨上,棒与导轨垂直并保持良好接触,整个装置处在垂直导轨平面向上的磁场中,若所加磁场的磁感应强度大小恒为B,使金属棒沿导轨由静止向下运动,金属棒运动的v-t图象如图(b)所示,当t=t0时刻,物体下滑距离为s.已知重力加速度为g,导轨电阻忽略不计.试求:
(2008?东莞模拟)如图(a)所示,两根足够长的光滑平行金属导轨相距为L,导轨平面与水平面成θ角,上端通过导线连接阻值为R的电阻,阻值为r的金属棒ab放在两导轨上,棒与导轨垂直并保持良好接触,整个装置处在垂直导轨平面向上的磁场中,若所加磁场的磁感应强度大小恒为B,使金属棒沿导轨由静止向下运动,金属棒运动的v-t图象如图(b)所示,当t=t0时刻,物体下滑距离为s.已知重力加速度为g,导轨电阻忽略不计.试求: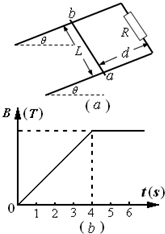 如图(a)所示,两根足够长、电阻不计的平行光滑金属导轨相距为L=1m,导轨平面与水平面成θ=30°角,上端连接R=1.5?的电阻;质量为m=0.2kg、阻值r=0.5?的金属棒ab放在两导轨上,距离导轨最上端为d=4m,棒与导轨垂直并保持良好接触.整个装置处于匀强磁场中,磁场方向与导轨平面垂直,磁感应强度大小随时间变化的情况如图(b)所示,前4s内为B=kt.前4s内,为保持ab棒静止,在棒上施加了一平行于导轨平面的外力F,已知当t=2s时,F恰好为零.求:
如图(a)所示,两根足够长、电阻不计的平行光滑金属导轨相距为L=1m,导轨平面与水平面成θ=30°角,上端连接R=1.5?的电阻;质量为m=0.2kg、阻值r=0.5?的金属棒ab放在两导轨上,距离导轨最上端为d=4m,棒与导轨垂直并保持良好接触.整个装置处于匀强磁场中,磁场方向与导轨平面垂直,磁感应强度大小随时间变化的情况如图(b)所示,前4s内为B=kt.前4s内,为保持ab棒静止,在棒上施加了一平行于导轨平面的外力F,已知当t=2s时,F恰好为零.求: