题目内容
质量为1kg的物块静止在水平面上，从某时刻开始对它施加大小为3N的水平推力，4s内物体的位移为16m，此时将推力突然反向但保持大小不变．求：（1）再经2s物体的速度多大？
（2）在前6s内推力对物体所做的总功为多少？
【答案】分析：物体初速度为零，经过4s时间位移为16m，可以用匀变速直线运动的位移时间关系式解出加速度，再根据牛顿第二定律解出物体受到的摩擦力以及推力方向后的加速度，最后由运动学关系式解出末速度；根据功的定义式解出推力对物体所做的总功．
解答：解：物体初速度为零，经过4s时间位移为16m，
由匀变速直线运动的位移时间关系式：x=
at2，
解得：a=2m/s2
此过程物体水平方向仅受向前的推力F与向后的摩擦力f，
根据牛顿第二定律有：F-f=ma
解得：f=1N
当推力反向时由牛顿第二定律得：F+f=ma1
得：a1=4m/s2
物体在4秒末物体速度：v=at=8m/s
推力反向t1=2s后的速度根据所速度时间关系式：v末=v-a1t1=0
所以再经2s物体速度为零．
（2）前4s内的位移x1=16m
后两秒内的位移：x2=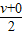
×2s=8m
在前6s内推力对物体所做的总功为
WF=Fx1-Fx2=24J
答：（1）再经2s物体的速度为0（2）在前6s内推力对物体所做的总功为24J
点评：注意在应用功能关系时解题思路一定要宽广，完全可以把功能关系与匀变速直线运动规律相结合来解题，这样就会使复杂的问题迎刃而解．
解答：解：物体初速度为零，经过4s时间位移为16m，
由匀变速直线运动的位移时间关系式：x=
at2，解得：a=2m/s2
此过程物体水平方向仅受向前的推力F与向后的摩擦力f，
根据牛顿第二定律有：F-f=ma
解得：f=1N
当推力反向时由牛顿第二定律得：F+f=ma1
得：a1=4m/s2
物体在4秒末物体速度：v=at=8m/s
推力反向t1=2s后的速度根据所速度时间关系式：v末=v-a1t1=0
所以再经2s物体速度为零．
（2）前4s内的位移x1=16m
后两秒内的位移：x2=
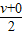×2s=8m在前6s内推力对物体所做的总功为
WF=Fx1-Fx2=24J
答：（1）再经2s物体的速度为0（2）在前6s内推力对物体所做的总功为24J
点评：注意在应用功能关系时解题思路一定要宽广，完全可以把功能关系与匀变速直线运动规律相结合来解题，这样就会使复杂的问题迎刃而解．
练习册系列答案
备战中考寒假系列答案
相关题目
在光滑的水平桌面上放着一块质量为M=10kg的木板，质量m=5kg的物块压在板上，它们间的摩擦系数为μ=0.1，物块与质量m'的重物由跨过滑轮的细绳（滑轮和细绳的质量和轮轴上的摩擦可忽略不计），连结如图．假设静摩擦系数等于滑动摩擦系数，都等于μ0．试分别计算：
（2013?福建模拟）如图1所示，质量足够大、截面是直角梯形的物块静置在光滑水平地面上，其两个侧面恰合与两个固定在地面上的压力传感器X和Y相接触，图AB高H=0.3m，AD长L=0.5m，斜面倾角θ=37°有一质量m=1kg的小物块p（图中未画出），它与斜面的动磨擦因数μ可以通过更换斜面的材料进行调节，调节范围是0≤μ≤1，取sin37°=0.6，cos37°=0.8，重力加速度g=10m/s2．
（1）2011年3月11日，日本东海岸发生9.0级地震，地震引发的海啸摧毁了日本福岛第一核电站的冷却系统，最终导致福岛第一核电站的6座核反应堆不同程度损坏，向空气中泄漏大量碘131和铯137等放射性物质，这些放射性物质随大气环流飘散到许多国家．4月4日，日本开始向太平洋排放大量带有放射性物质的废水，引起周边国家的指责．下列说法中正确的是：
如图所示，质量为1kg的物块放在倾角为37°的固定斜面上，若用一平行于斜面的力F推物块，物块和斜面保持静止，斜面与物块之间的最大静摩擦因数μ=0.5，重力加速度g取10m/s2，则外力F的大小可能为（ ）