题目内容
 在光滑的水平桌面上放着一块质量为M=10kg的木板,质量m=5kg的物块压在板上,它们间的摩擦系数为μ=0.1,物块与质量m'的重物由跨过滑轮的细绳(滑轮和细绳的质量和轮轴上的摩擦可忽略不计),连结如图.假设静摩擦系数等于滑动摩擦系数,都等于μ0.试分别计算:
在光滑的水平桌面上放着一块质量为M=10kg的木板,质量m=5kg的物块压在板上,它们间的摩擦系数为μ=0.1,物块与质量m'的重物由跨过滑轮的细绳(滑轮和细绳的质量和轮轴上的摩擦可忽略不计),连结如图.假设静摩擦系数等于滑动摩擦系数,都等于μ0.试分别计算:(1)当mˊ=0.4kg,
(2)当mˊ=1kg,两种条件下,物块和木板的加速度和它们间的相互作用力(g=10m/s2).
分析:先以木板为研究对象,求出它能够产生的最大加速度,再分析物块与木板之间有没有相对滑动,根据牛顿第二定律求解即可.
解答:解:先分析物块和木板发生相对滑动的条件.根据题设条件,木板能够产生的最大加速度为a′=
=
m/s2=0.5m/s2
仅当物块加速度a>a'时,物块和木板才能发生相对滑动.当a≤a′时,物块和木板保持相对静止a=a′时刚要发生相对滑动,这时重物的质量
可由牛顿第二定律建立下列方程解出:
T-(m+M)g=(m+M)a′
m0′g-T=m0′a′
解得
=
=
≈0.79(kg)
当m′≤m′0时,M与m间无相对滑动.
当m′>m′0时,M与m间有相对滑动.
(1)当mˊ=0.4kg<0.79kg,M与m间无相对滑动,可建立方程组得:a=
g=
×10≈0.26m/s2
此时M与m之间的压力为50N,静摩擦力为f=Ma=2.6N
(2)当mˊ=1kg>0.79kg,M与m间有相对滑动,它们之间的压力为50N,滑动摩擦力大小为f=μmg=5N
根据牛顿第二定律得:
m′g-T=ma′
T-μmg=ma
解得,a=
g=0.83m/s2
a′=
=0.5m/s2
答:
(1)当mˊ=0.4kg,M与m之间的压力为50N,静摩擦力为2.6N.加速度大小都是0.26m/s2
(2)当mˊ=1kg时,M与m间有相对滑动,它们之间的压力为50N,滑动摩擦力大小为5N.木板的加速度为0.83m/s2,物块的加速度为0.5m/s2.
| μ0mg |
| M |
| 0.1×5×10 |
| 10 |
仅当物块加速度a>a'时,物块和木板才能发生相对滑动.当a≤a′时,物块和木板保持相对静止a=a′时刚要发生相对滑动,这时重物的质量
| m | ′ 0 |
T-(m+M)g=(m+M)a′
m0′g-T=m0′a′
解得
| m | ′ 0 |
| (m+M)a′ |
| g-a′ |
| (5+10)×0.5 |
| 10-0.5 |
当m′≤m′0时,M与m间无相对滑动.
当m′>m′0时,M与m间有相对滑动.
(1)当mˊ=0.4kg<0.79kg,M与m间无相对滑动,可建立方程组得:a=
| m′ |
| m′+M+m |
| 0.4 |
| 0.4+5+10 |
此时M与m之间的压力为50N,静摩擦力为f=Ma=2.6N
(2)当mˊ=1kg>0.79kg,M与m间有相对滑动,它们之间的压力为50N,滑动摩擦力大小为f=μmg=5N
根据牛顿第二定律得:
m′g-T=ma′
T-μmg=ma
解得,a=
| m′-μm |
| m′+m |
a′=
| μmg |
| M |
答:
(1)当mˊ=0.4kg,M与m之间的压力为50N,静摩擦力为2.6N.加速度大小都是0.26m/s2
(2)当mˊ=1kg时,M与m间有相对滑动,它们之间的压力为50N,滑动摩擦力大小为5N.木板的加速度为0.83m/s2,物块的加速度为0.5m/s2.
点评:本题关键是根据牛顿第二定律求出物块和木板保持相对静止刚要发生相对滑动时重物的质量,分析物块与木板的状态,运用牛顿第二定律时要灵活选择研究对象,

练习册系列答案
相关题目
 (2011?双流县模拟)如图所示,长为L的木板A静止在光滑的水平桌面上,A的左端上方放有小物体B(可视为质点),一端连在B上的细绳,绕过固定在桌子边沿的定滑轮后,另一端连在小物体C上,设法用外力使A、B静止,此时C被悬挂着.A的右端距离滑轮足够远,C距离地面足够高.已知A的质量为6m,B的质量为3m,C的质量为m.现将C物体竖直向上提高距离2L,同时撤去固定A、B的外力.再将C无初速释放,当细绳被拉直时B、C速度的大小立即变成相等,由于细绳被拉直的时间极短,此过程中重力和摩擦力的作用可以忽略不计,细绳不可伸长,且能承受足够大的拉力.最后发现B在A上相对A滑行的最大距离为
(2011?双流县模拟)如图所示,长为L的木板A静止在光滑的水平桌面上,A的左端上方放有小物体B(可视为质点),一端连在B上的细绳,绕过固定在桌子边沿的定滑轮后,另一端连在小物体C上,设法用外力使A、B静止,此时C被悬挂着.A的右端距离滑轮足够远,C距离地面足够高.已知A的质量为6m,B的质量为3m,C的质量为m.现将C物体竖直向上提高距离2L,同时撤去固定A、B的外力.再将C无初速释放,当细绳被拉直时B、C速度的大小立即变成相等,由于细绳被拉直的时间极短,此过程中重力和摩擦力的作用可以忽略不计,细绳不可伸长,且能承受足够大的拉力.最后发现B在A上相对A滑行的最大距离为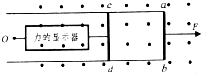 如图所示,在光滑的水平桌面上,放置一两边平行的质量为M,宽为L的足够长的“U”开金属框架,其框架平面与桌面平行.其ab部分的电阻为R,框架其它部分电阻不计.垂直框架两边放一质量为m、电阻为R的金属棒cd,它们之间的动摩擦因数为μ,且接触始终良好.cd棒通过不可伸长的细线与一个固定在O点力的显示器相连,始终处于静止状态.现在让框架由静止开始在水平恒定拉力F的作用下(F是未知数),向右做加速运动,设最大静摩擦力和滑动摩擦力相等.最终框架匀速运动时力的显示器的读数为2μmg.已知框架位于竖直向上足够大的匀强磁场中,磁感应强度为B.求
如图所示,在光滑的水平桌面上,放置一两边平行的质量为M,宽为L的足够长的“U”开金属框架,其框架平面与桌面平行.其ab部分的电阻为R,框架其它部分电阻不计.垂直框架两边放一质量为m、电阻为R的金属棒cd,它们之间的动摩擦因数为μ,且接触始终良好.cd棒通过不可伸长的细线与一个固定在O点力的显示器相连,始终处于静止状态.现在让框架由静止开始在水平恒定拉力F的作用下(F是未知数),向右做加速运动,设最大静摩擦力和滑动摩擦力相等.最终框架匀速运动时力的显示器的读数为2μmg.已知框架位于竖直向上足够大的匀强磁场中,磁感应强度为B.求 如图,在光滑的水平桌面上,静放着一质量为980g的长方形匀质木块,现有一颗质量为20g的子弹以300m/s的水平速度沿其轴线射向木块,结果子弹留在木块中没有射出,和木块一起以共同的速度运动.已知木块沿子弹运动方向的长度为10cm,子弹打进木块的深度为6cm.设木块对子弹的阻力保持不变.
如图,在光滑的水平桌面上,静放着一质量为980g的长方形匀质木块,现有一颗质量为20g的子弹以300m/s的水平速度沿其轴线射向木块,结果子弹留在木块中没有射出,和木块一起以共同的速度运动.已知木块沿子弹运动方向的长度为10cm,子弹打进木块的深度为6cm.设木块对子弹的阻力保持不变.
 。细绳始终在滑轮上,不计滑轮与细绳之间的摩擦,计算中可认为A、B之间的最大静摩擦力等于滑动摩擦力,取重力加速度g=10m/s2。
。细绳始终在滑轮上,不计滑轮与细绳之间的摩擦,计算中可认为A、B之间的最大静摩擦力等于滑动摩擦力,取重力加速度g=10m/s2。