题目内容
如图所示，在横截面半径为只的光滑圆柱体的两侧，用不可伸长的细绳悬挂着质量分别为
和
的A、B两个物体，开始时两物体与圆柱体的中心等高，并用手托住B物体后，突然释放，当A物体运动到圆柱体的最高点时，对圆柱体的压力是多大？
答案：略
解析：
解析：
|
选 A、B两物体初位置所在的平面为零势面，则系统的机械能 ，选物体到达圆柱体的最高点时为末态，并设此时A物体速度为v，由于绳不可伸长，显然B物体的速度大小也为v，则系统的机械能为  ，
由机械守恒定律有：  ，即： ，解得： ．A物体在圆柱体的最高点时，设圆柱体对A物体的支持力为 ，则由牛顿第二定律有： ，解得 ．由牛顿第三定律得，A物体运动到圆柱体的最高点时，对圆柱体的压力的大小为 ． |
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
（2013?重庆）利用半圆柱形玻璃，可减小激光束的发散程度．在如图所示的光路中，A为激光的出射点，O为半圆柱形玻璃横截面的圆心，AO过半圆顶点．若某条从A点发出的与AO成α角的光线，以入射角i入射到半圆弧上，出射光线平行于AO，求此玻璃的折射率．
（1）如图所示，竖直墙上挂着一面时钟，地面上静止的观察者A观察到钟的面积为S，另一观察者B以0.8倍光速平行y轴正方向运动，观察到钟的面积为S′．则S
如图所示，OBCD为半圆柱体玻璃的横截面，OD为直径，一束由红光和紫光组成的复色光沿AO方向从真空斜射入玻璃，B、C点为两单色光的射出点（设光线在B、C处未发生全反射）． 已知从B点射出的单色光由O到B的传播时间为t．求从C点射出的单色光由O到C的传播时间tC．
，
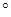MOA=60
，
MOA=60