题目内容
11. 如图所示,斜面倾角为θ,从斜面的P点分别以v0和2v0的速度水平抛出A、B两个小球,不计空气阻力,在两小球从开始运动到均落在斜面上时,下列说法正确的是( )
如图所示,斜面倾角为θ,从斜面的P点分别以v0和2v0的速度水平抛出A、B两个小球,不计空气阻力,在两小球从开始运动到均落在斜面上时,下列说法正确的是( )| A. | A、B两球的水平位移之比为1:2 | |
| B. | A、B两球飞行时间之比为1:3 | |
| C. | A、B两球下落的高度之比为1:2 | |
| D. | A、B两球落到斜面上时速度方向与斜面夹角之比为1:1 |
分析 以水平速度v0抛出一个小球,做平抛运动,落在斜面上时,根据竖直位移与水平位移的比值等于tanθ,求出运动的时间表达式,再得到水平位移、下落高度及落在斜面上时速度方向与水平方向的夹角表达式,即可分析.
解答 解:对于任意一球,小球落在斜面上时,有tanθ=$\frac{y}{x}$=$\frac{\frac{1}{2}g{t}^{2}}{{v}_{0}t}$=$\frac{gt}{2{v}_{0}}$,得 t=$\frac{2{v}_{0}tanθ}{g}$,则 t∝v0,故A、B两球飞行时间之比为1:2.
水平位移为 x=v0t=$\frac{2{v}_{0}^{2}tanθ}{g}$,则 x∝${v}_{0}^{2}$,故A、B两球的水平位移之比为1:4.
下落高度 h=$\frac{1}{2}g{t}^{2}$=$\frac{2{v}_{0}^{2}ta{n}^{2}θ}{g}$,故h∝${v}_{0}^{2}$,故A、B两球的下落高度之比为1:4.
设小球落在斜面上时速度与水平方向的夹角为α,则 tanα=$\frac{gt}{{v}_{0}}$=2tanθ,可知α是定值,与初速度大小无关,由几何知识知,两球落到斜面上时速度方向与斜面夹角相等,故ABC错误,D正确.
故选:D
点评 解决本题的关键掌握平抛运动的规律,知道平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,明确隐含的条件:竖直位移与水平位移的比值等于tanθ.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2. 如图所示,P、Q两物块叠放在一起,以相同的初速度竖直向下抛出.若P的质量大于Q的质量,不计空气阻力,则在物块下降过程中,下列说法正确的是( )
如图所示,P、Q两物块叠放在一起,以相同的初速度竖直向下抛出.若P的质量大于Q的质量,不计空气阻力,则在物块下降过程中,下列说法正确的是( )
 如图所示,P、Q两物块叠放在一起,以相同的初速度竖直向下抛出.若P的质量大于Q的质量,不计空气阻力,则在物块下降过程中,下列说法正确的是( )
如图所示,P、Q两物块叠放在一起,以相同的初速度竖直向下抛出.若P的质量大于Q的质量,不计空气阻力,则在物块下降过程中,下列说法正确的是( )| A. | Q所受的合外力等于Q受到的重力 | B. | Q所受的合外力小于Q受到的重力 | ||
| C. | P对Q的压力大于Q对P的支持力 | D. | P、Q间的弹力为零 |
6.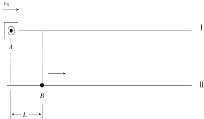 小明在某游乐训练场上练习移动打靶,如图所示,耙在Ⅰ号直线上以v0=10m/s的速度匀速向右移动,t1=0时刻耙在Ⅰ号直线上的A位置,在水平直线Ⅱ上距耙心水平距离L=25m的B处,小明坐在战车上从静止开始以a=2m/s2的加速度沿直线Ⅱ向右做匀加速直线运动,战车上的彩弹枪在战车静止时发出的彩弹速度v1=50m/s,Ⅰ、Ⅱ号水平直线的距离d=50m,sin37°=0.6.则( )
小明在某游乐训练场上练习移动打靶,如图所示,耙在Ⅰ号直线上以v0=10m/s的速度匀速向右移动,t1=0时刻耙在Ⅰ号直线上的A位置,在水平直线Ⅱ上距耙心水平距离L=25m的B处,小明坐在战车上从静止开始以a=2m/s2的加速度沿直线Ⅱ向右做匀加速直线运动,战车上的彩弹枪在战车静止时发出的彩弹速度v1=50m/s,Ⅰ、Ⅱ号水平直线的距离d=50m,sin37°=0.6.则( )
 小明在某游乐训练场上练习移动打靶,如图所示,耙在Ⅰ号直线上以v0=10m/s的速度匀速向右移动,t1=0时刻耙在Ⅰ号直线上的A位置,在水平直线Ⅱ上距耙心水平距离L=25m的B处,小明坐在战车上从静止开始以a=2m/s2的加速度沿直线Ⅱ向右做匀加速直线运动,战车上的彩弹枪在战车静止时发出的彩弹速度v1=50m/s,Ⅰ、Ⅱ号水平直线的距离d=50m,sin37°=0.6.则( )
小明在某游乐训练场上练习移动打靶,如图所示,耙在Ⅰ号直线上以v0=10m/s的速度匀速向右移动,t1=0时刻耙在Ⅰ号直线上的A位置,在水平直线Ⅱ上距耙心水平距离L=25m的B处,小明坐在战车上从静止开始以a=2m/s2的加速度沿直线Ⅱ向右做匀加速直线运动,战车上的彩弹枪在战车静止时发出的彩弹速度v1=50m/s,Ⅰ、Ⅱ号水平直线的距离d=50m,sin37°=0.6.则( )| A. | 欲使彩弹击中耙心,可在t=5.0s时发出彩弹 | |
| B. | 若彩弹在最短时间内击中靶心,则击中靶心时彩弹的速度是50m/s | |
| C. | 若要求在t=10.0s时发出彩弹并击中靶心,则彩弹枪与Ⅱ号水平直线的夹角(锐角)是53° | |
| D. | 若要求在t=10.0s时发出彩弹并击中靶心,则彩弹飞行的时间是0.5s |
16.汽车拉着拖车在平直的公路上运动,下面的说法错误的是( )
| A. | 汽车能拉着拖车前进是因为汽车对拖车的拉力大于拖车对汽车的拉力 | |
| B. | 汽车先对拖车施加拉力,然后才产生拖车对汽车的拉力 | |
| C. | 匀速前进时,汽车对拖车的拉力等于拖车向后拉汽车的力;加速前进时,汽车向前拉拖车的力大于拖车向后拉汽车的力 | |
| D. | 拖车加速前进时,是因为汽车对拖车的拉力大于地面对拖车的摩擦阻力,此时汽车对拖车向前的拉力等于拖车向后拉汽车的力 |
20.下列关于质点的说法中,正确的是( )
| A. | 质点是一个理想化模型,实际上并不存在 | |
| B. | 体积很小、质量很小的物体都可看成质点 | |
| C. | 质点和几何中的点没有区别 | |
| D. | 只有低速运动的物体才可看成质点,高速运动的物体不可看作质点 |
1.关于电场和磁场的描述正确的是( )
| A. | 磁感线和电场线都是闭合的曲线,且都是真实存在的 | |
| B. | 我们虽然摸不到电场的存在,却可以用小磁针取探测它的存在和强弱 | |
| C. | 电场强度的方向和电荷受力的方向相同,磁感应强度的方向与安培力的方向相同 | |
| D. | 电场强度和磁感应强度在国际单位制中的单位分别是V/m、N/A•m |
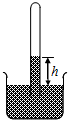 如图,开口向下的玻璃管插入水银槽中,管内封闭了一段气体,气体压强为p,管内外水银面高度差为h.若增大外界大气压强,则h将增大(增大、减小、不变);p将增大(增大、减小、不变)
如图,开口向下的玻璃管插入水银槽中,管内封闭了一段气体,气体压强为p,管内外水银面高度差为h.若增大外界大气压强,则h将增大(增大、减小、不变);p将增大(增大、减小、不变)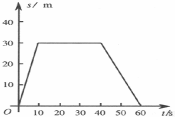 如图的x-t图象.0-10s物体做匀速直线运动,这段时间内物体的速度3m/s,10-40s物体静止,40-60s物体做匀速直线运动.这段时间里的速度为-3m/s.
如图的x-t图象.0-10s物体做匀速直线运动,这段时间内物体的速度3m/s,10-40s物体静止,40-60s物体做匀速直线运动.这段时间里的速度为-3m/s.