题目内容
17.质量为500t的机车以恒定的功率由静止出发.经5min行驶2.25km.速度达到的最大值54km/h,设阻力恒定,且取g=10m/s2,求:(1)机车的功率;
(2)机车的速度为36km/h时的加速度.
分析 (1)汽车达到速度最大时做匀速直线运动,牵引力做功为W=Pt,运用动能定理求解机车的功率P.
(2)根据匀速直线运动时的速度和功率,由P=Fv求出此时牵引力,即可得到阻力.当机车的速度为36km/h时,由P=Fv求出此时的牵引力,即可由牛顿第二定律求解加速度a
解答 解:(1)机车的最大速度为vm=54km/h=15m/s.
以机车为研究对象,机车从静止出发至达速度最大值过程,根据动能定理得:
Pt-fx=$\frac{1}{2}m{{v}_{m}}^{2}$
当机车达到最大速度时:P=Fvm=fvm
由以上两式得:P=3.75×105W
(2)机车匀速运动时,阻力为:$f=F=\frac{P}{{v}_{m}}=2.5×1{0}^{4}N$
当机车速度v=36 km/h=10m/s时机车的牵引力为:F1=$\frac{P}{v}$=3.75×104N
根据牛顿第二定律有:F1-f=ma
得:a=2.5×10-2m/s2
答:(1)机车的功率P是3.75×105W.
(2)机车的速度为36km/h时机车的加速度a为2.5×10-2m/s2.
点评 本题关键要清楚汽车启动的运动过程和物理量的变化,能够运用动能定理和牛顿第二定律解决问题,知道在额定功率下,当牵引力等于阻力时,速度达到最大.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
8. 如图所示,套在两光滑竖直杆上质量分别为mA、mB的小球A、B,由跨过定滑轮的轻细绳连接,静止时绳与竖直方向的夹角分别为α和β,不计一切摩擦.则下列关系正确的是( )
如图所示,套在两光滑竖直杆上质量分别为mA、mB的小球A、B,由跨过定滑轮的轻细绳连接,静止时绳与竖直方向的夹角分别为α和β,不计一切摩擦.则下列关系正确的是( )
 如图所示,套在两光滑竖直杆上质量分别为mA、mB的小球A、B,由跨过定滑轮的轻细绳连接,静止时绳与竖直方向的夹角分别为α和β,不计一切摩擦.则下列关系正确的是( )
如图所示,套在两光滑竖直杆上质量分别为mA、mB的小球A、B,由跨过定滑轮的轻细绳连接,静止时绳与竖直方向的夹角分别为α和β,不计一切摩擦.则下列关系正确的是( )| A. | mAsinα=mBsinβ | B. | mAsinβ=mBsinα | C. | mAcosα=mBcosβ | D. | mAcosβ=mBcosα |
12. 一物体放在一倾角为θ的斜面上,向下轻轻一推,它刚好能匀速下滑.若给此物体一个沿斜面向上的初速度v0,则它能上滑的最大路程是( )
一物体放在一倾角为θ的斜面上,向下轻轻一推,它刚好能匀速下滑.若给此物体一个沿斜面向上的初速度v0,则它能上滑的最大路程是( )
 一物体放在一倾角为θ的斜面上,向下轻轻一推,它刚好能匀速下滑.若给此物体一个沿斜面向上的初速度v0,则它能上滑的最大路程是( )
一物体放在一倾角为θ的斜面上,向下轻轻一推,它刚好能匀速下滑.若给此物体一个沿斜面向上的初速度v0,则它能上滑的最大路程是( )| A. | $\frac{{{v}_{0}}^{2}}{2g}$ | B. | $\frac{{{v}_{0}}^{2}}{2gsinθ}$ | C. | $\frac{{{v}_{0}}^{2}}{4gsinθ}$ | D. | $\frac{{{v}_{0}}^{2}}{2gcosθ}$ |
2. 一列横波在T=0时刻的波形如图中实线所示,在T=1s时刻波形如图中虚线所示.由此可以判定此波的( )
一列横波在T=0时刻的波形如图中实线所示,在T=1s时刻波形如图中虚线所示.由此可以判定此波的( )
 一列横波在T=0时刻的波形如图中实线所示,在T=1s时刻波形如图中虚线所示.由此可以判定此波的( )
一列横波在T=0时刻的波形如图中实线所示,在T=1s时刻波形如图中虚线所示.由此可以判定此波的( )| A. | 波长一定是4 cm | B. | 周期一定是4 s | ||
| C. | 振幅一定是4 cm | D. | 传播速度一定是1 cm/s |
9. 如图所示,质量为M的小车静止在光滑的水平面上.小车上AB部分是半径为R的四分之一光滑圆弧,BC部分是粗糙的水平面.今把质量为m的小物体从A点由静止释放,m与BC部分间的动摩擦因数为μ.最终小物体与小车相对静止于B、C之间的D点,则B、D间的距离s随各量变化的情况是( )
如图所示,质量为M的小车静止在光滑的水平面上.小车上AB部分是半径为R的四分之一光滑圆弧,BC部分是粗糙的水平面.今把质量为m的小物体从A点由静止释放,m与BC部分间的动摩擦因数为μ.最终小物体与小车相对静止于B、C之间的D点,则B、D间的距离s随各量变化的情况是( )
 如图所示,质量为M的小车静止在光滑的水平面上.小车上AB部分是半径为R的四分之一光滑圆弧,BC部分是粗糙的水平面.今把质量为m的小物体从A点由静止释放,m与BC部分间的动摩擦因数为μ.最终小物体与小车相对静止于B、C之间的D点,则B、D间的距离s随各量变化的情况是( )
如图所示,质量为M的小车静止在光滑的水平面上.小车上AB部分是半径为R的四分之一光滑圆弧,BC部分是粗糙的水平面.今把质量为m的小物体从A点由静止释放,m与BC部分间的动摩擦因数为μ.最终小物体与小车相对静止于B、C之间的D点,则B、D间的距离s随各量变化的情况是( )| A. | 其他量不变,R越大s越大 | B. | 其他量不变,μ越大s越大 | ||
| C. | 其他量不变,m越大s越大 | D. | 其他量不变,M越大s越大 |
6.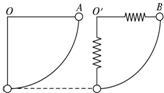 如图A、B两球质量相等,A球用不能伸长的轻绳系于O点,B球用轻弹簧系于O′点,O与O′点在同一水平面上,分别将A、B球拉到与悬点等高处,使绳和轻弹簧均处于水平,弹簧处于自然状态,将两球分别由静止开始释放,当两球达到各自悬点的正下方时,两球仍处在同一水平面上,则( )
如图A、B两球质量相等,A球用不能伸长的轻绳系于O点,B球用轻弹簧系于O′点,O与O′点在同一水平面上,分别将A、B球拉到与悬点等高处,使绳和轻弹簧均处于水平,弹簧处于自然状态,将两球分别由静止开始释放,当两球达到各自悬点的正下方时,两球仍处在同一水平面上,则( )
 如图A、B两球质量相等,A球用不能伸长的轻绳系于O点,B球用轻弹簧系于O′点,O与O′点在同一水平面上,分别将A、B球拉到与悬点等高处,使绳和轻弹簧均处于水平,弹簧处于自然状态,将两球分别由静止开始释放,当两球达到各自悬点的正下方时,两球仍处在同一水平面上,则( )
如图A、B两球质量相等,A球用不能伸长的轻绳系于O点,B球用轻弹簧系于O′点,O与O′点在同一水平面上,分别将A、B球拉到与悬点等高处,使绳和轻弹簧均处于水平,弹簧处于自然状态,将两球分别由静止开始释放,当两球达到各自悬点的正下方时,两球仍处在同一水平面上,则( )| A. | 两球到达各自悬点的正下方时,两球动能相等 | |
| B. | 两球到达各自悬点的正下方时,A球动能较大 | |
| C. | 两球到达各自悬点的正下方时,B球动能较大 | |
| D. | 两球到达各自悬点的正下方时,A球受到向上的拉力较小 |
