题目内容
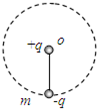 如图所示,一长为L的绝缘细线下端系质量为m的金属小球,并带有-q的电荷量,在细线的悬点o处放一带电荷量为+q的点电荷.要使金属球能在竖直平面内做完整的圆周运动,求:
如图所示,一长为L的绝缘细线下端系质量为m的金属小球,并带有-q的电荷量,在细线的悬点o处放一带电荷量为+q的点电荷.要使金属球能在竖直平面内做完整的圆周运动,求:(1)金属球在最高点的最小速度值是多大?
(2)如果金属球刚好通过最高点,则它通过最低点时的绳子拉力多大?
分析:(1)小球在最高点处当绳子拉力最小时,重力与库仑力充当向心力,由牛顿第二定律可求得最小速度;
(2)由动能定理可求得小球到达最低点的速度,再由牛顿第二定律求得最低点时的拉力.
(2)由动能定理可求得小球到达最低点的速度,再由牛顿第二定律求得最低点时的拉力.
解答:解:(1)小球在最高点绳子的拉力为零时速度最小,设最小速度为v1,则有牛顿第二定律可知:
mg+
=
解得:v1=
;
(2)小球从最高点到最低点的过程中,电场力做功为零;设最低点的速度为v2,据动能定理有:
2mgL=
mv22-
mv12
解得:v2=
由牛顿第二定律可得:
F2+
-mg=
解得:F2=6mg
答:(1)金属球在最高点的最小速度值是
;
(2)它通过最低点时的绳子拉力为6mg.
mg+
| Kq2 |
| L2 |
m
| ||
| L |
解得:v1=
gL+
|
(2)小球从最高点到最低点的过程中,电场力做功为零;设最低点的速度为v2,据动能定理有:
2mgL=
| 1 |
| 2 |
| 1 |
| 2 |
解得:v2=
5gL+
|
由牛顿第二定律可得:
F2+
| Kq2 |
| L2 |
m
| ||
| L |
解得:F2=6mg
答:(1)金属球在最高点的最小速度值是
gL+
|
(2)它通过最低点时的绳子拉力为6mg.
点评:本题考查动能定理及向心力公式,要注意最高点处临界值为绳子拉力为零时,此时小球有最小速度.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
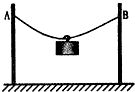 如图所示,一长为L的轻质细绳,固定于两竖直杆上A、B两点,A、B两点等高且杆间距为d<L.某人欲将质量为m的物体通过光滑的轻质挂钩从A处送到B处,他将挂钩从A处由静止释放,则( )
如图所示,一长为L的轻质细绳,固定于两竖直杆上A、B两点,A、B两点等高且杆间距为d<L.某人欲将质量为m的物体通过光滑的轻质挂钩从A处送到B处,他将挂钩从A处由静止释放,则( )| A、物体的运动轨迹是椭圆 | B、物体运动至绳中点时加速度为零 | C、物体在全过程的加速度是不变的 | D、物体不可能到达B处 |
 如图所示,一长为L的绝缘细线下端系一质量为m带电量为q的小球A,细线上端系在水平天花板的O点,在O点正下方固定一带电量为Q的小球B,在库仑力作用下A静止时细线拉力大小为T1,让B的电量变为2Q同时将细线从上端剪掉
如图所示,一长为L的绝缘细线下端系一质量为m带电量为q的小球A,细线上端系在水平天花板的O点,在O点正下方固定一带电量为Q的小球B,在库仑力作用下A静止时细线拉力大小为T1,让B的电量变为2Q同时将细线从上端剪掉 如图所示,一长为L的轻绳,一端固定在天花板上,另一端系一质量为m的小球,球绕竖直轴线O1O2在水平面内做匀速圆周运动,绳与竖直轴线间的夹角为θ,则下述说法中正确的是( )
如图所示,一长为L的轻绳,一端固定在天花板上,另一端系一质量为m的小球,球绕竖直轴线O1O2在水平面内做匀速圆周运动,绳与竖直轴线间的夹角为θ,则下述说法中正确的是( ) (2011?宜昌二模)如图所示,一长为L的薄壁玻璃管放置在水平面上,在玻璃管的a端放置一个直径比玻璃管直径略小的小球,小球带电荷量为-q、质量为m.玻璃管右边的空间存在方向竖直向上、磁感应强度为B的匀强磁场.磁场的左边界与玻璃管平行,右边界足够远.玻璃管带着小球以水平速度v0垂直于左边界向右运动,由于水平外力的作用,玻璃管进入磁场后速度保持不变,经一段时间后小球从玻璃管b端滑出并能在水平面内自由运动,最后从左边界飞离磁场.设运动过程中小球的电荷量保持不变,不计一切阻力.求:
(2011?宜昌二模)如图所示,一长为L的薄壁玻璃管放置在水平面上,在玻璃管的a端放置一个直径比玻璃管直径略小的小球,小球带电荷量为-q、质量为m.玻璃管右边的空间存在方向竖直向上、磁感应强度为B的匀强磁场.磁场的左边界与玻璃管平行,右边界足够远.玻璃管带着小球以水平速度v0垂直于左边界向右运动,由于水平外力的作用,玻璃管进入磁场后速度保持不变,经一段时间后小球从玻璃管b端滑出并能在水平面内自由运动,最后从左边界飞离磁场.设运动过程中小球的电荷量保持不变,不计一切阻力.求: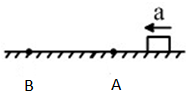 如图所示,一长为l的长方形木块在水平面上以加速度a做匀加速直线运动.A、B之间有一定的距离,木块前端P先到达A点,之后经过t1时间整个木块通过了A点,而前端P到达B点后,整个木块通过B点所用时间为t2.求:
如图所示,一长为l的长方形木块在水平面上以加速度a做匀加速直线运动.A、B之间有一定的距离,木块前端P先到达A点,之后经过t1时间整个木块通过了A点,而前端P到达B点后,整个木块通过B点所用时间为t2.求: