��Ŀ����
8�� ijͬѧ�������ͼ��ʾ��Ȥζʵ�����о���ײ���⣬�ò��Ϻͳ�����ͬ�IJ����쳤���������ν�N����С��ͬ���������ȵ�С��������ˮƽ�컨���·��������ڵ�С��ֹʱ�˴˽Ӵ��������������С���Ŵ���������Ϊ1��2��3������N��ÿ��С�������Ϊ���������С��������k����k��1�����ڵ�N��С���Ҳ���һ�⻬���������AB����ˮƽ�ģ�BCD������ֱ���ڵİ�Բ�Σ����ι⻬�����B��ƽ�����ӣ���Բ�����ֱ��BD����ֱ������ˮƽ�����A�˷���һ���N������С����ȫ��ͬ��PС������С������ĵȸߣ��ֽ�1��С������͵���������߶�h������������״̬�ɾ�ֹ�ͷ�1��С��ʹ����2��С����ײ��2��С������3��С����ײ����������ײ��Ϊ��ͬһֱ���ϵ���������е����ʧ����֪�������ٶ�Ϊg������������С��ÿ����ײʱ����ɺ��Բ��ƣ�
ijͬѧ�������ͼ��ʾ��Ȥζʵ�����о���ײ���⣬�ò��Ϻͳ�����ͬ�IJ����쳤���������ν�N����С��ͬ���������ȵ�С��������ˮƽ�컨���·��������ڵ�С��ֹʱ�˴˽Ӵ��������������С���Ŵ���������Ϊ1��2��3������N��ÿ��С�������Ϊ���������С��������k����k��1�����ڵ�N��С���Ҳ���һ�⻬���������AB����ˮƽ�ģ�BCD������ֱ���ڵİ�Բ�Σ����ι⻬�����B��ƽ�����ӣ���Բ�����ֱ��BD����ֱ������ˮƽ�����A�˷���һ���N������С����ȫ��ͬ��PС������С������ĵȸߣ��ֽ�1��С������͵���������߶�h������������״̬�ɾ�ֹ�ͷ�1��С��ʹ����2��С����ײ��2��С������3��С����ײ����������ײ��Ϊ��ͬһֱ���ϵ���������е����ʧ����֪�������ٶ�Ϊg������������С��ÿ����ײʱ����ɺ��Բ��ƣ���1����1��С����2��С����ײ֮ǰ���ٶ�v1�Ĵ�С��
��2����N=3�����3��С����PС������һ����ײǰ���ٶ�v3�Ĵ�С��
��3����N=5������Բ�ι���뾶R=$\frac{32}{5}$hʱ��PС���һ�α���ײ��ǡ����ͨ���������ߵ�D����kֵ�Ĵ�С��
���� 1������1��С����h���˶�����͵���̣����ݻ�е���غ������ǰ���ٶ�
2������1��2��С����ײ�Ĺ��̸��ݶ����غ㶨�ɺͻ�е���غ��г���ʽ������2��3��С����ײ�Ĺ��̣����ݶ����غ㶨�ɺͻ�е���غ����
3����Ϊ5��С����PС��������ȣ���֪���߷�����ײ���ٶȣ�����ţ�ٵڶ����ɵ�PС����D�ٶȣ�PС����A��D���˶����̣����ݻ�е���غ���⣮
��� �⣺��1����1��С�������Ϊm1����ǰ���ٶ�Ϊv1��
����1��С����h���˶�����͵���̣����ݻ�е���غ�
${m_1}gh=\frac{1}{2}{m_1}{v_1}^2$
��ã�${v_1}=\sqrt{2gh}$
��2����1�š�2��С����ײ����ٶȷֱ�Ϊv1���v2��ȡˮƽ����Ϊ������
����1��2��С����ײ�Ĺ��̣����ݶ����غ㶨����
m1v1=m1v'1+m2v2
���ݻ�е���غ��� $\frac{1}{2}{m_1}{v_1}^2=\frac{1}{2}{m_1}{v'_1}^2+\frac{1}{2}{m_2}{v_2}^2$
��ã�${v_2}=\frac{2}{1+k}\sqrt{2gh}$
��2�š�3��С����ײ����ٶȷֱ�Ϊv2���v3��
����2��3��С����ײ�Ĺ��̣����ݶ����غ㶨���� m2v2=m2v'2+m3v3
���ݻ�е���غ��� $\frac{1}{2}{m_2}{v_2}^2=\frac{1}{2}{m_2}{v'_2}^2+\frac{1}{2}{m_3}{v_3}^2$
ͬ���ɽ�ã�3��С��������ٶ� ${v_3}={��{\frac{2}{1+k}}��^2}\sqrt{2gh}$
��3��С����PС������һ����ײǰ���ٶȴ�С ${v_3}={��{\frac{2}{1+k}}��^2}\sqrt{2gh}$
��3���ɣ�2���еĽ������֪5��С��������ٶ� ${v_5}={��{\frac{2}{1+k}}��^4}\sqrt{2gh}$
��Ϊ5��С����PС��������ȣ���֪���߷�����ײ���ٶȣ�
����PС���һ�α���ײ����ٶ� ${v_P}={��{\frac{2}{1+k}}��^4}\sqrt{2gh}$
PС���һ�α���ײ��ǡ����ͨ��Բ�������ߵ�D������ͨ����ߵ���ٶ�ΪvD��
����ţ�ٵڶ�����PС����D����
${k^4}{m_1}g=\frac{{{k^4}{m_1}v_D^2}}{R}$
��ã�${v_D}=\sqrt{gR}$
PС����A��D���˶����̣���е���غ���
$\frac{1}{2}{m_5}v_P^2={m_5}g•2R+\frac{1}{2}{m_5}v_D^2$
��ã�${v_P}=\sqrt{5gR}$
��$R=\frac{32}{5}h$������ʽ������ã�$k=\sqrt{2}-1$
�𣺣�1��1��С����2��С����ײ֮ǰ���ٶ�v1�Ĵ�С��$\sqrt{2gh}$��
��2����N=3�����3��С����PС������һ����ײǰ���ٶ�v3�Ĵ�С��${��\frac{2}{1+k}��}^{2}\sqrt{2gh}$��
��3����N=5������Բ�ι���뾶R=$\frac{32}{5}$hʱ��PС���һ�α���ײ��ǡ����ͨ���������ߵ�D��kֵ�Ĵ�С��$\sqrt{2}$-1��
���� ���������ö����غ�ͻ�е���غ����Ͻ��һά��ײ����ĵ������ӣ�������1������ٶȹ��ɵ�n+1������ٶ��ǹؼ�������Ҳ���ѵ㣮

 ��ͼ��ʾ������������Ϊm��С��A��B�����ʵ������ӣ���ֹ���ڹ⻬ˮƽ���ϣ��ָ�С��Aһ�ٶ�v���ڵ��ɵ�һ�α�ѹ������̵Ĺ����У�����˵����ȷ���ǣ�������
��ͼ��ʾ������������Ϊm��С��A��B�����ʵ������ӣ���ֹ���ڹ⻬ˮƽ���ϣ��ָ�С��Aһ�ٶ�v���ڵ��ɵ�һ�α�ѹ������̵Ĺ����У�����˵����ȷ���ǣ�������| A�� | A��B������ܶ��ܲ��� | |
| B�� | A��B������ܶ���Ϊmv | |
| C�� | ���ɶ�B������������ڶ�A��������� | |
| D�� | ���ɱ�ѹ�������ʱ��A��B������ܶ�����С |
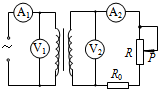 ��ͼ��ʾΪģ���ͷ��ѹ��ͨ����ѹ���û������ʾ��ͼ����ѹ������Ľ�����ѹ����Ϊ���䣮��ѹ������ĵ�ѹ������ͨ������������û�����ֵ����R0��ʾ����ߵĵ��裬������R��ʾ�û��õ������ܵ��裮����ѹ��Ϊ�����ѹ�������Ϊ�����������ڱ������Ļ�ƬP�����ƶ��Ĺ����У�������
��ͼ��ʾΪģ���ͷ��ѹ��ͨ����ѹ���û������ʾ��ͼ����ѹ������Ľ�����ѹ����Ϊ���䣮��ѹ������ĵ�ѹ������ͨ������������û�����ֵ����R0��ʾ����ߵĵ��裬������R��ʾ�û��õ������ܵ��裮����ѹ��Ϊ�����ѹ�������Ϊ�����������ڱ������Ļ�ƬP�����ƶ��Ĺ����У�������| A�� | V2ʾ����С | B�� | V1ʾ����� | C�� | A2ʾ����� | D�� | A1ʾ����С |
 ����ͼ��ʾ�ĵ�·�У�L1��L2��������ͬ��С���ݣ�A��B�������߿��ڸ�����һ����ѧԪ����a��b���˷ֱ���ֱ����Դ�ͽ�����Դ�����ӣ���ֱ����Դ�ĵ�ѹ�뽻����Դ��ѹ����Чֵ��ȣ��۲���������µ��ݵ����ȣ�����ֱ����Դʱ��L1�����⣬L2�������⣻���ӽ�����Դʱ��L1���⣬L2���Ա䰵��������˵����ȷ���ǣ�������
����ͼ��ʾ�ĵ�·�У�L1��L2��������ͬ��С���ݣ�A��B�������߿��ڸ�����һ����ѧԪ����a��b���˷ֱ���ֱ����Դ�ͽ�����Դ�����ӣ���ֱ����Դ�ĵ�ѹ�뽻����Դ��ѹ����Чֵ��ȣ��۲���������µ��ݵ����ȣ�����ֱ����Դʱ��L1�����⣬L2�������⣻���ӽ�����Դʱ��L1���⣬L2���Ա䰵��������˵����ȷ���ǣ�������| A�� | A�нӵ��ǵ��裬B�нӵ��ǵ����� | |
| B�� | A�нӵ��ǵ����Ȧ��B�нӵ��ǵ��� | |
| C�� | A�нӵ��ǵ����Ȧ��B�нӵ��ǵ����� | |
| D�� | A�нӵ��ǵ�������B�нӵ��ǵ����Ȧ |
 ��ͼ��ʾ��ˮƽ�����Ϸ����������ڴ��ڴ�ֱֽ���������ǿ�ų�����������ͬ���ϡ���ͬ��ϸ�ĵ������Ƶĵ��ѱպ���������Ȧl��2����߳�L1��L2���ھ�ų��Ͻ���h�ߴ��ɾ�ֹ��ʼ�������䣬������ȫ����ų�������䵽���森�˶������У���Ȧƽ��ʼ�ձ�������ֱƽ�������±�Եƽ���ڴų��ϱ߽磮����Ȧl��2���ʱ���ٶȴ�С�ֱ�Ϊv1��v2���ڴų����˶�ʱ�����������ֱ�ΪQ1��Q1��ͨ����Ȧ����ĵ�����ֱ�Ϊq1��q2�����ƿ���������������
��ͼ��ʾ��ˮƽ�����Ϸ����������ڴ��ڴ�ֱֽ���������ǿ�ų�����������ͬ���ϡ���ͬ��ϸ�ĵ������Ƶĵ��ѱպ���������Ȧl��2����߳�L1��L2���ھ�ų��Ͻ���h�ߴ��ɾ�ֹ��ʼ�������䣬������ȫ����ų�������䵽���森�˶������У���Ȧƽ��ʼ�ձ�������ֱƽ�������±�Եƽ���ڴų��ϱ߽磮����Ȧl��2���ʱ���ٶȴ�С�ֱ�Ϊv1��v2���ڴų����˶�ʱ�����������ֱ�ΪQ1��Q1��ͨ����Ȧ����ĵ�����ֱ�Ϊq1��q2�����ƿ���������������| A�� | v1��v2��Q1��Q2��q1��q2 | B�� | v1=v2��Q1=Q2��q1=q2 | ||
| C�� | v1��v2��Q1��Q2��q1=q2 | D�� | v1=v2��Q1��Q2��q1��q2 |
 ��ͼ��ʾ��������ɽ���������A������ĸ߶�H=45m��Բ�ι����ߴ���B������ĸ߶�h=30m������Ħ��������������ɽ����A���ɾ�ֹ��ʼ�»���gȡ10m/s2������
��ͼ��ʾ��������ɽ���������A������ĸ߶�H=45m��Բ�ι����ߴ���B������ĸ߶�h=30m������Ħ��������������ɽ����A���ɾ�ֹ��ʼ�»���gȡ10m/s2������


