Question

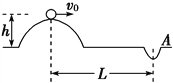
【题目】如图所示，一根轻绳一端固定在O点，另一端拴一质量m=0.1kg的小球静止于A点，其右方有底面半径r=0.2m的转筒，转筒顶端与A等高，筒底端左侧有一小孔，距顶端h=0.8m。开始时小球处于O点所在水平面上方30°的位置B处且细绳刚好伸直，OB及OA与转筒的轴线在同一竖直平面内，小孔此时也位于该竖直平面内。将小球从B点由静止释放，小球经过A点时速度vA=2m/s，此时轻绳突然断掉，同时转筒立刻以某一角速度做匀速转动，最终小球恰好进入小孔．取g=10m/s2，不计空气阻力。求：

(1)转筒轴线与A点的距离d；

(2)转筒转动的角速度ω；

(3)轻绳的长度L。

Answer 1

【答案】（1）1.99m（2）5n rad/s（n=1、2、3……）（3）0.8m

【解析】

(1)小球做平抛运动，由平抛运动的规律可求得水平距离。(2)根据运动的等时性可以求出圆筒的转动角速度。( 3 )由于绳子的作用，小球在绳了张紧时要用速度损失，故不能直接用小球的速度，而应用其垂直于绳子的分速度。

（1）小球平抛：

d≈1.99m

t=0.4s

（2）圆筒匀速圆周运动：

t=0.4s

rad/s（n=1、2、3……）

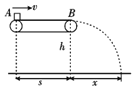
（3）如图所示，小球从B点由静止开始下落，做自由落体运动，一直运动到C点，轻绳中才出现张力，C点和B点关于水平线上下对称，则：

从C→A，根据动能定理得：

同理，从B→C

联立得：

L=0.8m