题目内容
16.如图a,轨道固定在竖直平面内,水平段的DE光滑、EF粗糙,EF段有一竖直挡板,ABCD光滑并与水平段平滑连接,ABC是以O为圆心的圆弧,B为圆弧最高点.物块P2静止于E处,物块P1从D点开始水平向右运动并与P2发生碰撞,且碰撞时间极短.已知:P1的质量m1=0.5kg,碰撞前后的位移图象如图b;P2的质量m2=1.8kg,与EF轨道之间的动摩擦因数μ=$\frac{5}{6}$,与挡板碰撞时无机械能损失;圆弧半径为R=$\frac{5}{12}$m; P1、P2可视为质点且运动紧贴轨道;取g=10m/s2.

(1)求P2被碰后获得的速度大小
(2)P1经过B时受到的支持力大小
(3)用L表示挡板与E的水平距离.若P2最终停在了EF段距离E为X的某处,试通过分析与计算,在图c中作出X-L图线.
分析 (1)由题图可求得对应的初速度,再由动量守恒定律可求得速度;
(2)由机械能守恒可求得P1到达B点时的速度,再由向心力公式可求得支持力;
(3)由题意明确相碰的条件,再通过分情况计论得出对应的图象.
解答 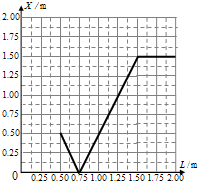 解:(1)根据s-t图象可知:P1的初速度为 v0=$\frac{1.5}{0.1}$=15m/s;①
解:(1)根据s-t图象可知:P1的初速度为 v0=$\frac{1.5}{0.1}$=15m/s;①
碰后速度为 v1=-3m/s②
设P2被碰后获得的速度为v2,有动量守恒:m1v0=m1v1+m2v2③
①②式并代入数据,得:v2=5m/s④
(2)设P1到B时的速度为vB,机械能守恒,有:$\frac{1}{2}{m_1}v_1^2=\frac{1}{2}{m_1}v_B^2+{m_1}gR$⑤
设P1通过B时轨道对它的支持力大小为F,有:${m_1}g-F=\frac{{{m_1}v_B^2}}{R}$⑥
由③④⑤式并代入数据,得:F=4.2N⑦
(3)P2与挡板碰后能停在EF段的条件是,P2不会从弯曲轨道飞出,设此时挡板距E的距离为L1,即:$\frac{1}{2}{m_2}v_2^2-μ{m_2}g•2{L_1}<{m_2}gR$⑧
设挡板距E的距离为L1时,P2与挡板能碰N次,此时满足:$\frac{1}{2}{m_2}v_2^2>μ{m_2}g•(2\right.N-\left.1){L_1}$⑨
⑧、⑨解得:L1>0.5m; N<2
由此可知,P2最终停在EF段的条件是:L≥0.5m;而且P2与挡板最多只碰一次⑩
(或者:由于$\frac{1}{2}{m_2}v_2^2≤3μ{m_2}g•{L_1}$,所以最多与挡板只碰一次)
分情况讨论如下:
(i)若P2与挡板没发生碰撞就已停下来,即:L≥X
功能关系,有:$\frac{1}{2}{m_2}v_2^2-μ{m_2}gX=0$(11)
代入数据得:X=1.5m,
即:当L≥1.5m时,X=1.5m(12)
(ii)若P2与挡板碰一次,且返回时未能到达E点,即:L<2L-X≤2L
功能关系,有:$\frac{1}{2}{m_2}v_2^2-μ{m_2}g(2L-X)=0$(13)
代入数据得:X=2L-1.5,
即当0.75m≤L<1.5m时,X=2L-1.5(14)
(ii)若P2与挡板碰一次,返回时过E点,经曲面后又再次进入EF段,即:2L≤2L+X≤3L功能关系,有:$\frac{1}{2}{m_2}v_2^2-μ{m_2}g(2L+X)=0$(15)
代入数据得:X=1.5-2L
即0.5m≤L≤0.75m时,X=1.5-2L(16)
S-L图线如图
答:(1)P2被碰后获得的速度大小为5m/s;
(2)P1经过B时受到的支持力大小为4.2N;
(3)X-L图线如图所示.
点评 本题考查动量守恒、机械能守恒等物理规律的应用,在解题中要注意认真分析物理过程,明确可能出现的情况,要学会对物体进行全面分析讨论.

 如图所示,一台模型发电机的电枢是矩形导线框ABCD,电枢绕垂直于磁场方向的线框对称中心线OO′匀速转动,通过电刷与一理想变压器连接,已知该变压器原线圈匝数n1=1000匝,副线圈匝数n2=200匝,副线圈中接一“44V,44W”的电动机,此时它正常工作.所有线圈及导线电阻不计,电表对电路的影响忽略不计,则下列说法正确的是( )
如图所示,一台模型发电机的电枢是矩形导线框ABCD,电枢绕垂直于磁场方向的线框对称中心线OO′匀速转动,通过电刷与一理想变压器连接,已知该变压器原线圈匝数n1=1000匝,副线圈匝数n2=200匝,副线圈中接一“44V,44W”的电动机,此时它正常工作.所有线圈及导线电阻不计,电表对电路的影响忽略不计,则下列说法正确的是( )| A. | 电压表的读数为220$\sqrt{2}$V | |
| B. | 若仅将矩形线圈变为圆形(线圈匝数、导线材料以及单匝长度不变),电压表示数将增大 | |
| C. | 图示时刻,磁通量最大,电动势为0,因此电压表的读数为0 | |
| D. | 若该电动机的内阻为8Ω,则它的输出功率为32W |
| A. | 结合能越小表示原子核中的核子结合得越牢固 | |
| B. | 太阳辐射的能量主要来自太阳内部的核裂变反应 | |
| C. | 235U的半衰期约为7亿年,随着全球气候变暖,其半衰期将变短 | |
| D. | 氢原子核外电子从半径较小的轨道跃迁到半径较大的轨道时,需要吸收能量 |
 2011年9月29日,中国首个空间实验室“天宫一号”在酒泉卫星发射中心发射升空,如图所示,由长征运载火箭送入近地点为A、远地点为B的椭圆轨道上,B点距地面高度为h,地球的中心位于椭圆的一个焦点上.“天宫一号”飞行数圈后变轨,进入预定圆轨道,已知“天宫一号”在预定圆轨道上飞行n圈所用时间为t,引力常量为G,地球半径为R.则下列说法正确的是( )
2011年9月29日,中国首个空间实验室“天宫一号”在酒泉卫星发射中心发射升空,如图所示,由长征运载火箭送入近地点为A、远地点为B的椭圆轨道上,B点距地面高度为h,地球的中心位于椭圆的一个焦点上.“天宫一号”飞行数圈后变轨,进入预定圆轨道,已知“天宫一号”在预定圆轨道上飞行n圈所用时间为t,引力常量为G,地球半径为R.则下列说法正确的是( )| A. | 由题中给出的信息可以计算出地球的质量为$\frac{4{π}^{2}{n}^{2}(R+h)^{2}}{G{t}^{2}}$ | |
| B. | “天宫一号”在椭圆轨道的B点的加速度小于在预定圆轨道的B点的加速度 | |
| C. | “天宫一号”从A点开始沿椭圆轨道向B点运行的过程中,其机械能守恒 | |
| D. | “天宫一号”从A点开始沿椭圆轨道向B点运行的过程中,其动能逐渐减小 |
 滑草运动是一项使用特定用具沿倾斜的草地滑行的运动.某旅游景区山坡滑草滑到如图所示,山坡倾角θ=37°.直滑道底端通过极小的弧形滑到连接半径R=100m的圆弧坡面,圆弧坡面底端水平.一名游客连同滑草用具总质量m=70kg,用具与坡面间的动摩擦因数μ=0.5.开始下滑阶段同伴对游客施加沿坡面向下的恒定推力F,经过时间t1=4s,游客滑过位移x=24m,此时撤去推力F,游客自然向下滑行,再经时间t2=10s滑到坡底.不计空气阻力和经过直滑道与圆弧坡面间的能量损失,取g=10m/s2,sin37°=0.6,cos37°=0.8.求:
滑草运动是一项使用特定用具沿倾斜的草地滑行的运动.某旅游景区山坡滑草滑到如图所示,山坡倾角θ=37°.直滑道底端通过极小的弧形滑到连接半径R=100m的圆弧坡面,圆弧坡面底端水平.一名游客连同滑草用具总质量m=70kg,用具与坡面间的动摩擦因数μ=0.5.开始下滑阶段同伴对游客施加沿坡面向下的恒定推力F,经过时间t1=4s,游客滑过位移x=24m,此时撤去推力F,游客自然向下滑行,再经时间t2=10s滑到坡底.不计空气阻力和经过直滑道与圆弧坡面间的能量损失,取g=10m/s2,sin37°=0.6,cos37°=0.8.求: 长为L的细线,拴一质量为m的小球,一端固定于O点,让其在水平面内做匀速圆周运动(这种运动通常称为圆锥运动),如图所示.当摆线L与竖直方向的夹角是α时,
长为L的细线,拴一质量为m的小球,一端固定于O点,让其在水平面内做匀速圆周运动(这种运动通常称为圆锥运动),如图所示.当摆线L与竖直方向的夹角是α时,
 为了精确测量一电动势约为5V,内阻约为2.5Ω的直流电源的电动势E和内电阻r,现在除提供导线若干、开关一个和待测电源外,还提供有如下仪器:
为了精确测量一电动势约为5V,内阻约为2.5Ω的直流电源的电动势E和内电阻r,现在除提供导线若干、开关一个和待测电源外,还提供有如下仪器: 如图所示,一辆拖车通过定滑轮将一重物G匀速提升,当拖车从A点水平移动到B点时,位移为s,绳子由竖直变为与竖直方向成θ的角度,求此过程中拖车对绳子所做的功.
如图所示,一辆拖车通过定滑轮将一重物G匀速提升,当拖车从A点水平移动到B点时,位移为s,绳子由竖直变为与竖直方向成θ的角度,求此过程中拖车对绳子所做的功.