题目内容
11. 如图所示,轻杆上固定着质量相等的小球a和b,杆可绕O点在竖直面内自由转动,oa=ab=L,先将杆拉到水平位置后由静止开始释放,求:
如图所示,轻杆上固定着质量相等的小球a和b,杆可绕O点在竖直面内自由转动,oa=ab=L,先将杆拉到水平位置后由静止开始释放,求:(1)轻杆转到竖直位置时a球的速率;
(2)在轻杆从水平位置转到竖直位置的过程中,a,b两球各自的机械能是增加了还是减少了?变化的数量是多少?
分析 (1)转动过程中,两球组成的系统只有重力做功,机械能守恒,根据机械能守恒定律和两球速度.
(2)在竖直方向时,对a和b进行受力分析,根据动能定理求出轻杆对ab所做的功,从而判断机械能的变化.
解答 解:(1)转动过程中,两球组成的系统只有重力做功,机械能守恒,则得:
mgL+mg•2L=$\frac{1}{2}m{{v}_{a}}^{2}+\frac{1}{2}m{{v}_{b}}^{2}$
两球的角速度相等,由v=ωr,得:vb=2va
联立以上解得:va=$\sqrt{\frac{6gL}{5}}$,vb=2$\sqrt{\frac{6gL}{5}}$
(2)设此过程杆对A、B做的功分别为Wa、Wb,对a、b分别据动能定理得:
$\frac{1}{2}m{{v}_{a}}^{2}=mgL{+W}_{a}$,
$\frac{1}{2}m{{v}_{b}}^{2}=2mgL{+W}_{b}$,
解得:${W}_{a}=-\frac{2}{5}mgL$,${W}_{b}=\frac{2}{5}mgL$,
根据功能关系可知,机械能的变化量等于除重力以外的力做的功,即ab两球机械能的变化量等于杆子对两球做的功,则a的机械能减少$\frac{2}{5}mgL$,b的机械能增加$\frac{2}{5}mgL$.
答:(1)轻杆转到竖直位置时a球的速率为$\sqrt{\frac{6gL}{5}}$;
(2)在轻杆从水平位置转到竖直位置的过程中,a的机械能减少$\frac{2}{5}mgL$,b的机械能增加$\frac{2}{5}mgL$.
点评 本题主要考查了机械能守恒定律、动能定理的直接应用,列式时要知道ab两球的角速度相等,此题物理过程较复杂,难度适中.

练习册系列答案
相关题目
2. 从同一地点同时开始沿同一方向做直线运动的两个物体Ⅰ、Ⅱ的速度图象如图所示.在0-t0时间内,下列说法中正确的是( )
从同一地点同时开始沿同一方向做直线运动的两个物体Ⅰ、Ⅱ的速度图象如图所示.在0-t0时间内,下列说法中正确的是( )
 从同一地点同时开始沿同一方向做直线运动的两个物体Ⅰ、Ⅱ的速度图象如图所示.在0-t0时间内,下列说法中正确的是( )
从同一地点同时开始沿同一方向做直线运动的两个物体Ⅰ、Ⅱ的速度图象如图所示.在0-t0时间内,下列说法中正确的是( )| A. | Ⅰ、Ⅱ两个物体所受的合外力都在不断减小 | |
| B. | Ⅰ物体所受的合外力不断增大,Ⅱ物体所受的合外力不断减小 | |
| C. | Ⅰ物体的位移不断增大,Ⅱ物体的位移不断减小 | |
| D. | Ⅰ物体的平均速度小于$\frac{{v}_{1}+{v}_{2}}{2}$,Ⅱ物体的平均速度大于$\frac{{v}_{1}+{v}_{2}}{2}$ |
6.在“测定匀变速直线运动的加速度”的实验中,如果电源的频率稍微减小从而导致打点的周期稍微变大了一点,而实验者并不知情,则( )
| A. | 它将导致实验者测量的相邻计数点之间的间隔变大,从而使测得的加速度偏大 | |
| B. | 它将导致实验者用公式vn=$\frac{{x}_{n}+{x}_{n+1}}{2T}$求得的各计数点对应的瞬时速度偏大,从而用v-t图象处理数据时导致测得的加速度偏大 | |
| C. | 它将导致实验者用公式vn=$\frac{{x}_{n}+{x}_{n+1}}{2T}$求得的各计数点对应的瞬时速度偏小,从而用v-t图象处理数据时导致测得的加速度偏小 | |
| D. | 用逐差法处理数据时,由于代入的T的数据偏小,从而导致测得的加速度偏大 |
4.一质点做简谐运动的振动图象如图所示,质点的速度与加速度方向相同的时间段是( )
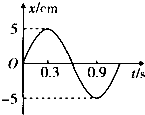

| A. | 0~O.3s | B. | 0~O.6s | C. | 0.6~O.9s | D. | 0.9~1.2s |
5. 如图所示,在光滑的桌面上有M、m两个物块,现用水平力F推物块m,使M、m两物块在桌上一起向右加速,则M、m间的相互作用力为( )
如图所示,在光滑的桌面上有M、m两个物块,现用水平力F推物块m,使M、m两物块在桌上一起向右加速,则M、m间的相互作用力为( )
 如图所示,在光滑的桌面上有M、m两个物块,现用水平力F推物块m,使M、m两物块在桌上一起向右加速,则M、m间的相互作用力为( )
如图所示,在光滑的桌面上有M、m两个物块,现用水平力F推物块m,使M、m两物块在桌上一起向右加速,则M、m间的相互作用力为( )| A. | $\frac{mF}{M+m}$ | |
| B. | $\frac{MF}{M+m}$ | |
| C. | 若物块与桌面的摩擦因数均为μ,M、m仍向右加速,则M、m间的相互作用力为$\frac{MF}{M+m}$+μMg | |
| D. | 若物块桌面的摩擦因数均为μ,M、m仍向右加速,则M、m间的相互作用力仍为$\frac{MF}{M+m}$ |

 如图所示,质量M=4kg的木板静置于光滑水平面上,质量m=1kg的小物块(可视为质点)以初速度v0=4m/s从木板的左端冲上木板,同时在木板的右端施加一个水平向右F=2N的恒力,经t=1s撤去外力,最后小物块恰好不从木板的上端滑下,已知小物块与木板之间的动摩擦因数μ=0.2,重力加速度g=10m/s2,求:
如图所示,质量M=4kg的木板静置于光滑水平面上,质量m=1kg的小物块(可视为质点)以初速度v0=4m/s从木板的左端冲上木板,同时在木板的右端施加一个水平向右F=2N的恒力,经t=1s撤去外力,最后小物块恰好不从木板的上端滑下,已知小物块与木板之间的动摩擦因数μ=0.2,重力加速度g=10m/s2,求: