题目内容
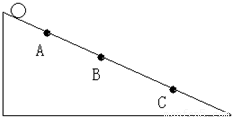一小球从静止开始沿斜面以恒定的加速度滚下来，依次通过A、B、C三点，已知AB=12m，BC=20m，小球通过AB、BC所用的时间均为2s，则：（1）求出小球下滑时的加速度？
（2）小球通过A、B、C三点时的速度分别是多少？
（3）斜面A点以上部分至少有多长？
【答案】分析：球沿斜面向下做匀加速直线运动，根据推论△x=aT2求出加速度，用推论求出小球经过B点时的瞬时速度，再根据速度时间公式求出A、C两点的速度．由速度位移关系求出斜面A点以上部分的长度．
解答：解：（1）小球沿斜面向下做匀加速直线运动，则有：BC-AB=aT2
得到：a=
．
（2）小球经过B点时的瞬时速度为：vB=
．
则：vA=vB-aT=8-2×2m/s=4m/s．
vC=vB+aT=8+2×2m/s=12m/s．
（3）根据：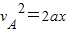
得：x=
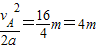
答：（1）求出小球下滑时的加速度2m/s2．
（2）小球通过A、B、C三点时的速度分别是4m/s、8m/s、12m/s．
（2）斜面A点以上部分至少有4m．
点评：本题关键在于匀变速直线运动两大推论的应用．也可以运用基本公式列方程组求解．中等难度．
解答：解：（1）小球沿斜面向下做匀加速直线运动，则有：BC-AB=aT2
得到：a=
．（2）小球经过B点时的瞬时速度为：vB=
．则：vA=vB-aT=8-2×2m/s=4m/s．
vC=vB+aT=8+2×2m/s=12m/s．
（3）根据：
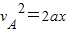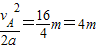
得：x=答：（1）求出小球下滑时的加速度2m/s2．
（2）小球通过A、B、C三点时的速度分别是4m/s、8m/s、12m/s．
（2）斜面A点以上部分至少有4m．
点评：本题关键在于匀变速直线运动两大推论的应用．也可以运用基本公式列方程组求解．中等难度．
练习册系列答案
相关题目
一个质量为M劈形物体abc，各面均光滑，放在固定的倾角为θ足够长的斜面上，ab表面成水平，bc高为h．ab面上中点放一质量为m光滑小球，今把物体abc从静止开始释放，则小球在碰到斜面以前的运动轨迹和碰到斜面时的速度是（ ）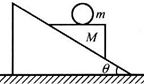
如图所示，一个劈形物体M放存固定的粗糙斜面上，其上面呈水平．在其水平面上放一光滑小球m．当劈形物体从静止开始释放后，观察到m和M有相对运动，则小球m在碰到斜面前的运动轨迹是（ ）
如图，一个楔形物体M放在固定的粗糙斜面上，上表面水平，在其上表面上放一光滑小球m，楔形物体从静止开始释放，则小球在碰到斜面前的运动轨迹是（ ）
如图所示，在倾角为θ的光滑斜面上，放有两个质量分别为m和2m的可视为质点的小球A和B，两球之间用一根长为L的轻杆相连，小球B到水平面的高度为h．两球从静止开始下滑，不计球与地面碰撞时的机械能损失，且地面光滑，当地的重力加速度为g．试求：