题目内容
 一个质量为M劈形物体abc,各面均光滑,放在固定的倾角为θ足够长的斜面上,ab表面成水平,bc高为h.ab面上中点放一质量为m光滑小球,今把物体abc从静止开始释放,则小球在碰到斜面以前的运动轨迹和碰到斜面时的速度是( )
一个质量为M劈形物体abc,各面均光滑,放在固定的倾角为θ足够长的斜面上,ab表面成水平,bc高为h.ab面上中点放一质量为m光滑小球,今把物体abc从静止开始释放,则小球在碰到斜面以前的运动轨迹和碰到斜面时的速度是( )分析:物体做什么样的运动取决于物体的受力由于速度方向的关系,同一条直线上就是直线运动,否则就是曲线运动.根据系统的机械能守恒和小球与物体abc速度关系,求解小球碰到斜面时的速度.
解答:解:由于劈形物体abc的水平面是光滑的,当斜面体abc在光滑的斜面上下滑时,小球由于只在竖直方向受力,故小球在碰到斜面之前的运动轨迹是竖直向下的直线.
设小球碰到斜面时的速度大小为v,物体abc速度大小为V,根据系统的机械能守恒得:
mg
=
mv2+
MV2
又两者速度的关系为v=Vsinθ
联立解得,v=
故选D.
设小球碰到斜面时的速度大小为v,物体abc速度大小为V,根据系统的机械能守恒得:
mg
| h |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又两者速度的关系为v=Vsinθ
联立解得,v=
|
故选D.
点评:由于各个面都是光滑的,所以物体只受重力,就是竖直向下的直线运动.关键是运用系统的机械能守恒和速度关系求解小球的速度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
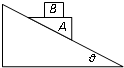 如图,在光滑的倾角为θ的固定斜面上放一个劈形的物体A,质量为M,其上表面水平且粗糙.质量为m的物体B放在A的上面,AB能保持相对静止并一起沿斜面下滑,求
如图,在光滑的倾角为θ的固定斜面上放一个劈形的物体A,质量为M,其上表面水平且粗糙.质量为m的物体B放在A的上面,AB能保持相对静止并一起沿斜面下滑,求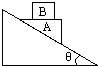 如图,在光滑的倾角为θ的固定斜面上放一个劈形的物体A,其上表面水平,质量为M.物体B质量为m,B放在A的上面,先用手固定住A.
如图,在光滑的倾角为θ的固定斜面上放一个劈形的物体A,其上表面水平,质量为M.物体B质量为m,B放在A的上面,先用手固定住A.
