题目内容
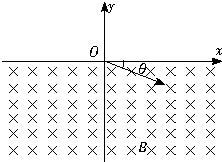如图所示，在y＜0的区域内存在匀强磁场，磁场方向垂直于xy平面并指向纸里，磁感应强度为B．一带负电的粒子（质量为m、电荷量为q）以速度v0从O点射入磁场，入射方向在xy平面内，与x轴正向的夹角为θ．求：该粒子射出磁场的位置（粒子所受重力不计）分析：画出带电粒子在磁场中的运动轨迹，根据洛伦兹力提供向心力求出半径，结合几何关系即可求出该粒子射出磁场的位置．
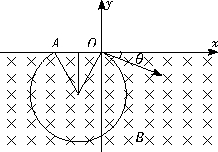
解答：解：带负电粒子射入磁场后，由于受到洛伦兹力的作用，粒子将沿图示的轨迹运动，从A点射出磁场，设O、A间的距离为L，射出时速度的大小仍为v，射出方向与x轴的夹角仍为θ，由洛伦兹力公式和牛顿定律可得：
qv0B=m
式中R为圆轨道半径，解得：
R=
圆轨道的圆心位于OA的中垂线上，由几何关系可得：
=Rsinθ
联解①②两式，得：L=
所以粒子离开磁场的位置坐标为（-
，0）
答：该粒子射出磁场的位置坐标为（-
，0）．
qv0B=m
| ||
| R |
式中R为圆轨道半径，解得：
R=
| mv0 |
| qb |
圆轨道的圆心位于OA的中垂线上，由几何关系可得：
| L |
| 2 |
联解①②两式，得：L=
| 2mv0sinθ |
| qB |
所以粒子离开磁场的位置坐标为（-
| 2mv0sinθ |
| qb |
答：该粒子射出磁场的位置坐标为（-
| 2mv0sinθ |
| qb |
点评：利用圆的特性构建几何关系，并运用由洛伦兹力提供向心力的物理规律列出方程，从而联立求解．
练习册系列答案
相关题目
如图所示，在y＞0的空间中存在着沿y轴正方的匀强电场；在y＜0的空间中存在垂直xoy平面向里的匀强磁场．一个带负电的粒子（质量为m，电荷量为q，不计重力），从y轴上的P（0，b）点以平行于x轴的初速度υ0射入电场，经过x轴上的N（2b，0）点．求：
如图所示，在y＜0的区域内存在匀强磁场，磁场方向垂直于xy平面并指向纸里，磁感应强度为B．一带负电的粒子（质量为m、电荷量为q）以速度v0从O点射入磁场，入射方向在xy平面内，与x轴正向的夹角为θ．求：
（2008?西城区一模）如图所示，在y＞0的区域内有沿y轴正方向的匀强电场，在y＜0的区域内有垂直坐标平面向里的匀强磁场．一电子（质量为m、电量为e）从y轴上A点以沿x轴正方向的初速度v0开始运动．当电子第一次穿越x轴时，恰好到达C点；当电子第二次穿越x轴时，恰好到达坐标原点；当电子第三次穿越x轴时，恰好到达D点．C、D两点均未在图中标出．已知A、C点到坐标原点的距离分别为d、2d．不计电子的重力．求：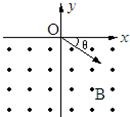
如图所示，在y＜0的区域内存在匀强磁场，磁场方向垂直于xoy平面并指向纸面外，磁感应强度为B．一带正电的粒子以速度v0从O点射入磁场，入射方向在xoy平面内，与x轴正向的夹角为θ．若粒子射出磁场的位置与O点的距离为l，求该粒子的电量和质量之比q/m及带点粒子在磁场中的运动时间．