题目内容
12. 某兴趣小组准备探究“合外力做功和物体速度变化的关系”,实验前组员们提出了以下几种猜想:
某兴趣小组准备探究“合外力做功和物体速度变化的关系”,实验前组员们提出了以下几种猜想:①W∝v;②W∝v2;③W∝$\sqrt{v}$;④W∝(△v)2.
为了验证猜想,他们设计了如图甲所示的实验装置.PQ为一块倾斜放置的木板,在Q处固定一个速度传感器(用来测量物体每次通过Q点的速度).在刚开始实验时,小刚同学提出“不需要测出物体质量,只要测出物体初始位置到速度传感器的距离L和读出速度传感器的读数v就行了”,大家经过讨论采纳了小刚的建议.
(1)请你说明小刚建议根据动能定理列出方程式,可以简化约去质量m;
(2)让物体分别从不同高度无初速释放,测出物体初始位置到速度传感器的距离L1、L2、L3、L4…,读出物体每次通过Q点的速度v1、v2、v3、v4、…,并绘制了如图乙所示的L-v图象.若为了更直观地看出L和v的变化关系,他们下一步应该作出A;
A.L-v2图象 B.L-$\sqrt{v}$图象 C.L-$\frac{1}{v}$图象D.L-$\frac{1}{{\sqrt{v}}}$图象
(3)实验中,木板与物体间摩擦力不会(“会”或“不会”)影响探究的结果.
分析 通过实验来探究“合外力做功和物体速度变化的关系”.每次实验物体从不同初位置处静止释放,量出初位置到速度传感器的位移、读出物体到传感器位置的速度.根据实验数据列出数据表并描点作出图象,从而找到位移与速度变化的关系,在运动过程中,由于物体受力是恒定的,所以得出合外力做功与物体速度变化的关系.因此在实验中物体与木板间的摩擦力不会影响探究的结果.
解答 解:(1)若只有重力做功,则:mgmgLsin=$\frac{1}{2}m{v}^{2}$,等号的两边都有m,可以约掉,故不需要测出物体的质量.用牛顿第二定律求解,也能得出相同的结论.
若是重力和摩擦力做功,则:$(mgsinθ-μmgcosθ)L=\frac{1}{2}m{v}^{2}$,等号的两边都有m,可以约掉,故不需要测出物体的质量.用牛顿第二定律求解,也能得出相同的结论.
(2)采用表格方法记录数据,合理绘制的L-v图象是曲线,不能得出结论W∝v2.为了更直观地看出L和v的变化关系,应该绘制L-v2图象.
故选:A
(3)重力和摩擦力的总功W也与距离L成正比,因此不会影响探究的结果.
故答案为:(1)根据动能定理列出方程式,可以简化约去质量m;(2)A;(3)不会.
点评 通过实验数据列表、描点、作图从而探究出问题的结论.值得注意的是:由于合外力恒定,因此合外力做的功与发生的位移是成正比.故可先探究位移与速度变化有何关系.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
15.如图所示,固定在水平面上的光滑斜面底端有一固定挡板,一轻弹簧下端连接在挡板上,上端和置于斜面上的物块P相连.物块P通过轻绳绕过轻质光滑定滑轮与粗糙水平面上的物块Q相连,系统处于静止时,物块P、Q的受力个数可能是( )


| A. | P受3个力、Q受2个力 | B. | P受3个力、Q受3个力 | ||
| C. | P受4个力、Q受3个力 | D. | P受4个力、Q受4个力 |
 如图,用“碰撞实验器”可以验证动量守恒定律,即研究两个小球在轨道水平部分碰撞前后的动量关系.
如图,用“碰撞实验器”可以验证动量守恒定律,即研究两个小球在轨道水平部分碰撞前后的动量关系. 光滑的$\frac{1}{4}$圆弧轨道固定在竖直平面内,与水平轨道CE连接.水平轨道的CD段光滑、DE段粗糙.一根轻质弹簧一端固定在C处的竖直面上,弹簧处于自然长度.将质量为m的物块a从顶端F点静止释放后,沿圆弧轨道下滑.
光滑的$\frac{1}{4}$圆弧轨道固定在竖直平面内,与水平轨道CE连接.水平轨道的CD段光滑、DE段粗糙.一根轻质弹簧一端固定在C处的竖直面上,弹簧处于自然长度.将质量为m的物块a从顶端F点静止释放后,沿圆弧轨道下滑.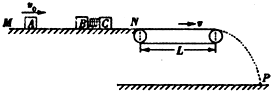 如图所示为某种弹射装置的示意图,光滑的水平导轨MN右端N处与水平传送带理想连接,传送带长度L=4.0m,皮带轮沿顺时针方向转动,带动皮带以恒定速率v=3.0m/s匀速传动.三个质量均为m=1.0kg的滑块A、B、C置于水平导轨上,开始时滑块B、C之间用细绳相连,中间有一压缩的轻弹簧,处于静止状态,滑块A以初速度v0=2.0m/s沿B、C连线方向向B运动,A与B碰撞后粘合在一起,碰撞时间极短,可认为A与B碰撞过程中滑块C的速度仍为零.因碰撞使连接B、C的细绳受扰动而突然断开,弹簧伸展,从而使C与A、B分离.滑块C脱离弹簧后以速度 vC=2.0m/s滑上传送带,并从右端滑出落至地面上的P点,已知滑块C与传送带之间的动摩擦因数μ=0.20,重力加速度g取10m/s2.求:
如图所示为某种弹射装置的示意图,光滑的水平导轨MN右端N处与水平传送带理想连接,传送带长度L=4.0m,皮带轮沿顺时针方向转动,带动皮带以恒定速率v=3.0m/s匀速传动.三个质量均为m=1.0kg的滑块A、B、C置于水平导轨上,开始时滑块B、C之间用细绳相连,中间有一压缩的轻弹簧,处于静止状态,滑块A以初速度v0=2.0m/s沿B、C连线方向向B运动,A与B碰撞后粘合在一起,碰撞时间极短,可认为A与B碰撞过程中滑块C的速度仍为零.因碰撞使连接B、C的细绳受扰动而突然断开,弹簧伸展,从而使C与A、B分离.滑块C脱离弹簧后以速度 vC=2.0m/s滑上传送带,并从右端滑出落至地面上的P点,已知滑块C与传送带之间的动摩擦因数μ=0.20,重力加速度g取10m/s2.求: 如图所示,倾角为α的光滑固定斜面,斜面上相隔为d的平行虚线MN与PQ间有大小为B的匀强磁场,方向垂直斜面向下.一质量为m,电阻为R,边长为L的度v匀速进入磁场,线圈ab边刚进入磁场和cd边刚要离开磁场时,ab边两端的电压相等.已知磁场的宽度d大于线圈的边长L,重力加速度为g.求
如图所示,倾角为α的光滑固定斜面,斜面上相隔为d的平行虚线MN与PQ间有大小为B的匀强磁场,方向垂直斜面向下.一质量为m,电阻为R,边长为L的度v匀速进入磁场,线圈ab边刚进入磁场和cd边刚要离开磁场时,ab边两端的电压相等.已知磁场的宽度d大于线圈的边长L,重力加速度为g.求



 如图所示,一质量M=20kg横截面积S=2×10-3m2的活塞封闭一定质量的理想气体,气缸壁导热良好,摩擦不计,当气体的温度由17℃缓慢增为27℃时活塞上升了1cm;现保持气体温度27℃不变,在活塞上面缓慢加上m=10kg的细沙,求此时活塞离气缸底部的高度.(取g=10m/s2,大气压强po=1.0×105pa)
如图所示,一质量M=20kg横截面积S=2×10-3m2的活塞封闭一定质量的理想气体,气缸壁导热良好,摩擦不计,当气体的温度由17℃缓慢增为27℃时活塞上升了1cm;现保持气体温度27℃不变,在活塞上面缓慢加上m=10kg的细沙,求此时活塞离气缸底部的高度.(取g=10m/s2,大气压强po=1.0×105pa)