题目内容
4. 如图所示,两根光滑的平行金属导轨MN、PQ处于同一水平面内,相距L=0.5m,导轨的左端用R=3Ω的电阻相连,导轨电阻不计,导轨上跨接一电阻r=1Ω的金属杆ab,质量m=0.2kg,整个装置放在竖直向上的匀强磁场中,磁感应强度B=2T,现对杆施加水平向右的拉力F=2N,使它由静止开始运动,求:
如图所示,两根光滑的平行金属导轨MN、PQ处于同一水平面内,相距L=0.5m,导轨的左端用R=3Ω的电阻相连,导轨电阻不计,导轨上跨接一电阻r=1Ω的金属杆ab,质量m=0.2kg,整个装置放在竖直向上的匀强磁场中,磁感应强度B=2T,现对杆施加水平向右的拉力F=2N,使它由静止开始运动,求:(1)杆能达到的最大速度多大?
(2)若已知杆从静止开始运动至最大速度的过程中,R上总共产生了10.2J的电热,则此过程中金属杆ab的位移多大?
(3)接(2)问,此过程中流过电阻R的电量?经历的时间?
分析 (1)杆速度最大时,拉力与安培力平衡,根据安培力表达式求出杆的最大速度;
(2)拉力F做的功一是转变为杆的动能和电阻R上产生的电热,据此计算杆ab位移的大小;
(3)q=$\frac{△Φ}{R+r}$求解通过电阻R的电量,安培力的冲量I=BILt=Bqt,根据动量定理求此过程经历的时间.
解答 解:(1)由题意得,当杆速度最大时,杆水平方向受到的拉力与安培力平衡,即满足:
F=BIL
又根据欧姆定律可得I=$\frac{E}{R+r}=\frac{BL{v}_{max}}{R+r}$
代入可得:$F=\frac{{B}^{2}{L}^{2}{v}_{max}}{R+r}$
可得杆的最大速度为:${v}_{max}=\frac{F(R+r)}{{B}^{2}{L}^{2}}=\frac{2(3+1)}{{2}^{2}×0.{5}^{2}}m/s=8m/s$
(2)根据能量转化和守恒定律有,拉力F对杆做的功等于杆获得的动能和电路上产生的电热之和,故有:
因为R和r串联,所以有:$\frac{{Q}_{R}}{R}=\frac{{Q}_{r}}{r}$
可得:${Q}_{r}=\frac{r}{R}{Q}_{R}=\frac{1}{3}10.2J=3.4J$
所以有:Fs=$\frac{1}{2}m{v}^{2}+{Q}_{R}+{Q}_{r}$
可得杆产生的位移:$s=\frac{\frac{1}{2}m{v}^{2}+{Q}_{R}+{Q}_{r}}{F}=\frac{\frac{1}{2}×0.2×{8}^{2}+10.2+3.4}{2}m$=10m
(3)流过电阻的电量为:
$q=I•t=\frac{△Φ}{R+r}=\frac{BLs}{R+r}=\frac{2×0.5×10}{3+1}C=2.5C$
该过程杆在水平方向由动量定理有:
Ft-BILt=mv-0
又It=q
所以有:Ft-qLB=mv
所以作用时间为:t=$\frac{mv+qLB}{F}=\frac{0.2×8+2.5×0.5×2}{2}s=2.05s$
答:(1)杆能达到的最大速度为8m/s;
(2)若已知杆从静止开始运动至最大速度的过程中,R上总共产生了10.2J的电热,则此过程中金属杆ab的位移为10m;
(3)此过程中流过电阻R的电量为2.5C,经历的时间为2.05s.
点评 本题一要能正确分析杆的受力情况和运动情况,此过程类似于汽车的起动;二要熟记感应电量表达式量q=$\frac{△Φ}{R+r}$,通过此式可以求解杆滑行的距离和时间.

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 平面MN、PQ、ST为三个相互平行的界面,Ⅰ、Ⅱ、Ⅲ为三种不同的介质,平面ST的上表面涂有反射层(光线不能通过).某种单色光线射向界面MN后,发生了一系列的反射和折射现象,光路如图所示.则( )
平面MN、PQ、ST为三个相互平行的界面,Ⅰ、Ⅱ、Ⅲ为三种不同的介质,平面ST的上表面涂有反射层(光线不能通过).某种单色光线射向界面MN后,发生了一系列的反射和折射现象,光路如图所示.则( )| A. | 当入射角β适当减小时,光线c、d都可能会消失 | |
| B. | 当入射角β适当增大时,光线d可能会消失 | |
| C. | 对于三种介质,光在介质Ⅱ中的传播速度最小 | |
| D. | 出射光线b、c、d不一定平行 |
| U/V | 0.00 | 2.56 | 2.71 | 2.80 | 2.84 | 2.87 | 2.89 | 2.91 | 2.99 |
| I/A | 0.00 | 0.03 | 0.07 | 0.11 | 0.34 | 0.52 | 0.75 | 0.91 | 3.02 |
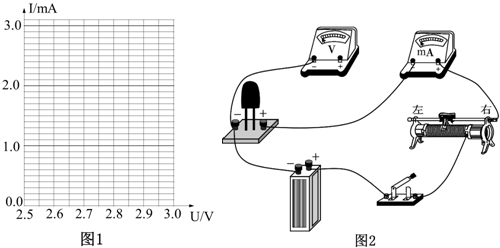
(1)根据以上数据,在图1中画出电压在2.5V〜3.00V范围内二极管的I-U图线.分析曲线可知二极管的电阻随U变大而变小(填‘变大”、“变小”或“不变”),在该范围内电阻最小约为1000Ω;
(2)某同学用伏安法测电阻的电路验证该二极管的伏安特性曲线,要求二极管的正向电压从0开始变化,并使测量误差尽量減小.图2是实验器材实物图,电压表量程为3V,内阻约为3kΩ,电流表量程为5mA,内阻约为10Ω.图中已连接了部分导线,请按实验要求将实物图中的连线补充完整.
(3)若此LED发光二极管的工作电流为2mA,则此发光二极管应与一阻值R=10Ω的电阻串联后才能与电动势为3V、内阻不计的电源相连.

| A. | 750Ω | B. | 760Ω | C. | 1000Ω | D. | 1010Ω |
 如图所示,通电直导线ab位于两平行导线横截面MN的连线的中垂线上,当平行导线通以同向等值电流时,以下说法中正确的是( )
如图所示,通电直导线ab位于两平行导线横截面MN的连线的中垂线上,当平行导线通以同向等值电流时,以下说法中正确的是( )| A. | 导线ab顺时针旋转 | B. | 导线a端向外,b端向里旋转 | ||
| C. | 导线ab逆时针旋转 | D. | 导线a端向里,b端向外旋转 |
 一列周期为T的简谐横波沿x轴的某一方向传播,已知t=0时刻的波形如图所示,此时平衡位置位于x=3m处的质点正在向上运动.若a、b两质点平衡位置的坐标分别为xa=2.5m,xb=5.5m,则( )
一列周期为T的简谐横波沿x轴的某一方向传播,已知t=0时刻的波形如图所示,此时平衡位置位于x=3m处的质点正在向上运动.若a、b两质点平衡位置的坐标分别为xa=2.5m,xb=5.5m,则( )| A. | 当a质点处在波峰时,b质点恰在波谷 | |
| B. | t=$\frac{T}{4}$时,a质点正在向y轴负方向运动 | |
| C. | t=$\frac{3T}{4}$时,b质点正在向y轴负方向运动 | |
| D. | 任何时刻a、b两质点的速度都不可能相同 |
| A. | 一定质量的气体被压缩时,气体压强一定增大 | |
| B. | 分子力总是随着分子间距离的增大而减小 | |
| C. | 外界对物体做功,物体同时从外界吸热,物体的内能可能减小 | |
| D. | 一定质量的气体,当分子热运动变剧烈时,压强可以不变 |
 如图所示,一质量为1kg的长木板放在水平桌面上,木板与桌面间的最大静摩擦力为3.0N,动摩擦因数为0.3.在木板被水平推力推动的过程中,当木板伸出桌面$\frac{1}{3}$时,木板受到的摩擦力为多大?
如图所示,一质量为1kg的长木板放在水平桌面上,木板与桌面间的最大静摩擦力为3.0N,动摩擦因数为0.3.在木板被水平推力推动的过程中,当木板伸出桌面$\frac{1}{3}$时,木板受到的摩擦力为多大?