题目内容
11. 一细杆与水桶相连,水桶中装有水,水桶与细杆一起在竖直平面内做圆周运动,如图所示,水的质量m=0.5kg,水的重心到转轴的距离l=50cm.
一细杆与水桶相连,水桶中装有水,水桶与细杆一起在竖直平面内做圆周运动,如图所示,水的质量m=0.5kg,水的重心到转轴的距离l=50cm.(1)若在最高点水不流出来,求桶的最小速率;
(2)若在最高点水桶的速率v=3m/s,求水对桶底的压力.
分析 (1)以水桶中的水为研究对象,在最高点恰好不流出来,说明水的重力恰好提供其做圆周运动所需的向心力,根据牛顿运动定律列式求解;
(2)桶中的水为研究对象,对它进行受力分析,找出它做圆周运动所需向心力的来源,根据牛顿运动定律建立方程即解.
解答 解:(1)以水桶中的水为研究对象,在最高点恰好不流出来,说明水
的重力恰好提供其做圆周运动所需的向心力,此时桶的速率最小.
此时有:mg=m$\frac{{v}^{2}}{r}$
则所求的最小速率为:v0=$\sqrt{gr}$=$\sqrt{10×0.5}$=2.42m/s
(2)在最高点,水所受重力mg的方向竖直向下,此时水具有向下的向心加速度,处于失重状态,其向心加速度的大小由桶底对水的压力和水的重力决定.
由向心力公式F=m$\frac{{v}^{2}}{r}$知,当v增大时,物体做圆周运动所需的向心力也随之增大,由于v=3m/s>v0=2.42m/s,因此,当水桶在最高点时,水所受重力已不足以水做圆周运动所需的向心力,此时桶底对水有一向下的压力,设为FN,则由牛顿第二定律有:
FN+mg=m$\frac{{v}^{2}}{r}$
即FN=m$\frac{{v}^{2}}{r}$-mg
代入数据可得FN=2.6N.
答:(1)若在最高点水不流出来,桶的最小速率为2.42m/s;
(2)若在最高点水桶的速率v=3m/s,水对桶底的压力为2.6N.
点评 解决圆周运动的动力学问题,关键分析物体受力,确定向心力的来源,再运用牛顿第二定律列式求解即可,注意弹力的方向,对绳模型注意最高点只能是向下的弹力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.物体做平抛运动,其初速度未知,运动一定时间,下列说法错误的是( )
| A. | 物体下落的高度与初速度无关 | B. | 物体重力的冲量与初速度无关 | ||
| C. | 物体重力做功与初速度无关 | D. | 物体位移与初速度无关 |
19. 如图所示,a、b是一对平行的金属板,分别接到直流电源的两极上,右边有一档板,正中间开有一小孔d.在较大的空间范围内存在着匀强磁场,磁感应强度大小为B,方向垂直纸面向里,而在a、b两板间还存在着匀强电场.从两板左侧正中的中点c处射入一束正离子,这些正离子都沿直线运动到右侧,从d孔射出后分成3束.则这些正离子的 (重力忽略)( )
如图所示,a、b是一对平行的金属板,分别接到直流电源的两极上,右边有一档板,正中间开有一小孔d.在较大的空间范围内存在着匀强磁场,磁感应强度大小为B,方向垂直纸面向里,而在a、b两板间还存在着匀强电场.从两板左侧正中的中点c处射入一束正离子,这些正离子都沿直线运动到右侧,从d孔射出后分成3束.则这些正离子的 (重力忽略)( )
 如图所示,a、b是一对平行的金属板,分别接到直流电源的两极上,右边有一档板,正中间开有一小孔d.在较大的空间范围内存在着匀强磁场,磁感应强度大小为B,方向垂直纸面向里,而在a、b两板间还存在着匀强电场.从两板左侧正中的中点c处射入一束正离子,这些正离子都沿直线运动到右侧,从d孔射出后分成3束.则这些正离子的 (重力忽略)( )
如图所示,a、b是一对平行的金属板,分别接到直流电源的两极上,右边有一档板,正中间开有一小孔d.在较大的空间范围内存在着匀强磁场,磁感应强度大小为B,方向垂直纸面向里,而在a、b两板间还存在着匀强电场.从两板左侧正中的中点c处射入一束正离子,这些正离子都沿直线运动到右侧,从d孔射出后分成3束.则这些正离子的 (重力忽略)( )| A. | 速度一定都相同 | B. | 质量一定有3种不同的数值 | ||
| C. | 电量一定有3种不同的数值 | D. | 比荷($\frac{q}{m}$)一定相同数值 |
6. 如图所示,轻绳一端系一小球,另一端固定于O点,在O点正下方的P点钉一颗钉子,使悬线拉紧与竖直方向成一角度θ,然后由静止释放小球,当悬线碰到钉子时( )
如图所示,轻绳一端系一小球,另一端固定于O点,在O点正下方的P点钉一颗钉子,使悬线拉紧与竖直方向成一角度θ,然后由静止释放小球,当悬线碰到钉子时( )
 如图所示,轻绳一端系一小球,另一端固定于O点,在O点正下方的P点钉一颗钉子,使悬线拉紧与竖直方向成一角度θ,然后由静止释放小球,当悬线碰到钉子时( )
如图所示,轻绳一端系一小球,另一端固定于O点,在O点正下方的P点钉一颗钉子,使悬线拉紧与竖直方向成一角度θ,然后由静止释放小球,当悬线碰到钉子时( )| A. | 小球的瞬时速度突然变大 | B. | 小球的加速度突然变大 | ||
| C. | 球的所受的向心力突然变小 | D. | 悬线所受的拉力突然变大 |
16.如图为两分子系统的势能Ep与两分子间距离r的关系曲线.下列说法正确的是( )


| A. | 当r大于r1时,分子间的作用力表现为引力 | |
| B. | 当r小于r1时,分子间的作用力表现为斥力 | |
| C. | 当r等于r2时,分子间的作用力为零 | |
| D. | 在r由r1变到r2的过程中,分子间的作用力做正功 |
3.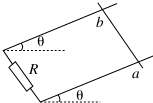 处于竖直向上的匀强磁场中的两根电阻不计的平行金属导轨,下端连一电阻R,导轨与水平面之间的夹角为θ.一电阻可忽略的金属棒ab,开始固定在两导轨上某位置,棒与导轨垂直,如图所示.现释放金属棒让其由静止开始沿轨道平面下滑.对导轨光滑和粗糙两种情况进行比较,当两次下滑的位移相同时,则有( )
处于竖直向上的匀强磁场中的两根电阻不计的平行金属导轨,下端连一电阻R,导轨与水平面之间的夹角为θ.一电阻可忽略的金属棒ab,开始固定在两导轨上某位置,棒与导轨垂直,如图所示.现释放金属棒让其由静止开始沿轨道平面下滑.对导轨光滑和粗糙两种情况进行比较,当两次下滑的位移相同时,则有( )
 处于竖直向上的匀强磁场中的两根电阻不计的平行金属导轨,下端连一电阻R,导轨与水平面之间的夹角为θ.一电阻可忽略的金属棒ab,开始固定在两导轨上某位置,棒与导轨垂直,如图所示.现释放金属棒让其由静止开始沿轨道平面下滑.对导轨光滑和粗糙两种情况进行比较,当两次下滑的位移相同时,则有( )
处于竖直向上的匀强磁场中的两根电阻不计的平行金属导轨,下端连一电阻R,导轨与水平面之间的夹角为θ.一电阻可忽略的金属棒ab,开始固定在两导轨上某位置,棒与导轨垂直,如图所示.现释放金属棒让其由静止开始沿轨道平面下滑.对导轨光滑和粗糙两种情况进行比较,当两次下滑的位移相同时,则有( )| A. | 重力势能的减小量相同 | B. | 机械能的变化量相同 | ||
| C. | 磁通量的变化量相同 | D. | 安培力做功相同 |
20.下列叙述中符合物理学史实的有( )
| A. | 德布罗意提出了实物粒子也具有波动性 | |
| B. | 玻尔通过α粒子散射实验,提出了原子的核式结构学说 | |
| C. | 汤姆生发现了质子 | |
| D. | 居里夫妇首先发现了天然放射现象 |