题目内容
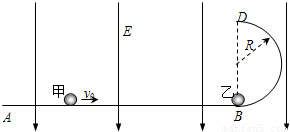
如图,ABD为竖直平面内的光滑绝缘轨道,其中AB段是水平的,BD段为半径R=0.2m的半圆,两段轨道相切于B点,整个轨道处在竖直向下的匀强电场中,场强大小E=5.0×103V/m.一不带电的绝缘小球甲,以速度υ沿水平轨道向右运动,与静止在B点带正电的小球乙发生弹性碰撞.已知乙球的质量为m=1.0×10-2kg,乙所带电荷量q=2.0×10-5C,甲球质量为乙球质量的k倍,g取10m/s2.(水平轨道足够长,甲、乙两球可视为质点,整个运动过程无电荷转移)(1)若k=1,且甲乙两球碰撞后,乙恰能通过轨道的最高点D,求甲的速度υ;
(2)若k>1,且甲仍以(1)中的速度υ向右运动,求乙在轨道上的首次落点到B点的距离范围.
【答案】分析:(1)由于两个球发生的是弹性碰撞,所以动量守恒,机械能也守恒,列出方程可以求出甲的速度v;
(2)对乙受力分析,乙离开最高点之后,做类平抛运动,竖直方向上匀加速运动,水平方向上匀速运动;乙求经过D点后的最小的速度应该是vD,再由动量守恒分析可得最大的速度,根据平抛运动水平方向的运动规律,可以求得范围的大小.
解答:解:(1)在乙恰能通过轨道的最高点的情况下,设乙到达最高点的速度为vD,乙离开D点到达水平轨道的时间为t,乙的落点到B点的距离为x,则
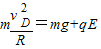 ①
①
设碰撞后甲、乙的速度分别为v甲、v乙,
根据动量守恒有:
kmv=kmv甲+mv乙 ②
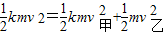 ③
③
联立②③得: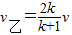 ④
④
由k=1,则v乙=v
由动能定理得: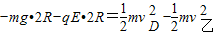 ⑤
⑤
联立①④⑤得: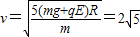 m/s ⑥
m/s ⑥
(2)甲、乙完全弹性碰撞,碰撞后甲、乙的速度分别为v甲、v乙,由②③得
解得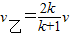 ⑦
⑦
又k>1,则v<v乙<2v ⑧
设乙球过D点的速度为vD′,由动能定理得
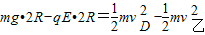 ⑨
⑨
解得:2m/s<vD′<8m/s ⑩
设乙在水平轨道上的落点到B点的距离为x′,则有:
x′=vD′t
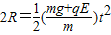
联立解得:0.4m≤x'<1.6m
答:(1)甲的速度是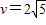 m/s;
m/s;
(2)乙在轨道上的首次落点到B点的距离范围是0.4m≤x′<1.6m.
点评:在本题中物体不仅受重力的作用,还有电场力,在解题的过程中,一定要分析清楚物体的受力和运动过程,两球在碰撞过程中动量守恒,碰后机械能守恒,题目中物体的运动过程比较复杂,在解题是一定分析清楚运动过程.
(2)对乙受力分析,乙离开最高点之后,做类平抛运动,竖直方向上匀加速运动,水平方向上匀速运动;乙求经过D点后的最小的速度应该是vD,再由动量守恒分析可得最大的速度,根据平抛运动水平方向的运动规律,可以求得范围的大小.
解答:解:(1)在乙恰能通过轨道的最高点的情况下,设乙到达最高点的速度为vD,乙离开D点到达水平轨道的时间为t,乙的落点到B点的距离为x,则
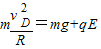 ①
①设碰撞后甲、乙的速度分别为v甲、v乙,
根据动量守恒有:
kmv=kmv甲+mv乙 ②
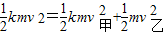 ③
③联立②③得:
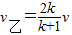 ④
④由k=1,则v乙=v
由动能定理得:
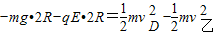 ⑤
⑤联立①④⑤得:
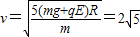 m/s ⑥
m/s ⑥(2)甲、乙完全弹性碰撞,碰撞后甲、乙的速度分别为v甲、v乙,由②③得
解得
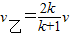 ⑦
⑦又k>1,则v<v乙<2v ⑧
设乙球过D点的速度为vD′,由动能定理得
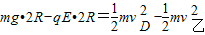 ⑨
⑨解得:2m/s<vD′<8m/s ⑩
设乙在水平轨道上的落点到B点的距离为x′,则有:
x′=vD′t
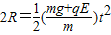
联立解得:0.4m≤x'<1.6m
答:(1)甲的速度是
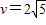 m/s;
m/s;(2)乙在轨道上的首次落点到B点的距离范围是0.4m≤x′<1.6m.
点评:在本题中物体不仅受重力的作用,还有电场力,在解题的过程中,一定要分析清楚物体的受力和运动过程,两球在碰撞过程中动量守恒,碰后机械能守恒,题目中物体的运动过程比较复杂,在解题是一定分析清楚运动过程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2011?绍兴二模)一端弯曲的光滑绝缘杆ABD固定在竖直平面上,如图所示,AB段水平,BD段是半径为R的半圆弧,有电荷量为Q(Q>0)的点电荷固定在圆心O点.一质量为m、电荷量为q(q>0)的带电小环套在光滑绝缘杆上,在水平外力作用下从C点由静此开始运动,到B点时撤去外力,小环继续运动,发现刚好能到绝缘杆的最高点D.已知CB间距为4R/3.(提示:根据电磁学有关知识,在某一空间放一电荷量为Q的点电荷,则距离点电荷为r的某点的电势为
(2011?绍兴二模)一端弯曲的光滑绝缘杆ABD固定在竖直平面上,如图所示,AB段水平,BD段是半径为R的半圆弧,有电荷量为Q(Q>0)的点电荷固定在圆心O点.一质量为m、电荷量为q(q>0)的带电小环套在光滑绝缘杆上,在水平外力作用下从C点由静此开始运动,到B点时撤去外力,小环继续运动,发现刚好能到绝缘杆的最高点D.已知CB间距为4R/3.(提示:根据电磁学有关知识,在某一空间放一电荷量为Q的点电荷,则距离点电荷为r的某点的电势为 一端弯曲的光滑绝缘轨道ABD固定在竖直平面上,如图所示,AB段水平、BD段是半径为R的半圆弧,有电荷量为Q的正点电荷固定在圆心O处.一质量为m、电荷量为q的带正电小环,在水平恒力F0作用下从C点由静止开始运动,到B点时撤去外力,小环继续运动,发现刚好能到达绝缘轨道上与圆心等高的M点,已知CB间距为
一端弯曲的光滑绝缘轨道ABD固定在竖直平面上,如图所示,AB段水平、BD段是半径为R的半圆弧,有电荷量为Q的正点电荷固定在圆心O处.一质量为m、电荷量为q的带正电小环,在水平恒力F0作用下从C点由静止开始运动,到B点时撤去外力,小环继续运动,发现刚好能到达绝缘轨道上与圆心等高的M点,已知CB间距为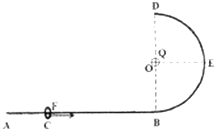 一端弯曲的光滑绝缘杆ABD固定在竖直平面上,如图所示,AB段水平,BD段是半径为R的半圆弧,有一电荷量为Q的正点电荷固定在圆心O点.一质量为m、电荷量为q的带正电小环套在光滑绝缘杆上,在大小为F的水平恒力作用下从C点由静止开始运动,到B点时撤去恒力,小环继续运动到达D点,已知CB间距为
一端弯曲的光滑绝缘杆ABD固定在竖直平面上,如图所示,AB段水平,BD段是半径为R的半圆弧,有一电荷量为Q的正点电荷固定在圆心O点.一质量为m、电荷量为q的带正电小环套在光滑绝缘杆上,在大小为F的水平恒力作用下从C点由静止开始运动,到B点时撤去恒力,小环继续运动到达D点,已知CB间距为 ,其中k为静电力常量,设无穷远处电势为零)。
,其中k为静电力常量,设无穷远处电势为零)。
