题目内容
质量为M=2.5kg的一只长方体形状的铁箱在水平拉力F作用下沿水平面向右匀加速运动，铁箱与水平面间的动摩擦因数为μ1=0.50。这时铁箱内一个质量为m=0.5kg的木块恰好能静止在后壁上(如图所示)，木块与铁箱内壁间的动摩擦因数为μ2=0.25。设最大静摩擦力等于滑动摩擦力，g取10m/s2。
求：(1)木块对铁箱的压力；
(2)水平拉力F的大小；
(3)使拉力F减小到120N，经过一段时间，木块落至箱底后且不反弹，某时刻当箱的速度为v=6m/s时撤去拉力，经1s时间木块从左侧到达右侧，则铁箱长度是多少？
（1）－20N 方向水平向左（2）135N（3）L=1.5m
【解析】
试题分析：（1）木块在竖直方向,由相对静止得 mg=Ff=μ2FN ∴FN=mg/μ2=5/0.25=20N
由牛顿第三定律得：木块对铁箱的压力FN/=－FN=－20N ,方向水平向左。- ①
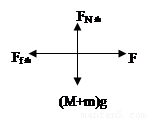
（2）对木块：在水平方向：FN=ma ∴a=20/0.5=40m/s2
对铁箱和木块整体：F－μ1(M+m)g =(M+m)a
故水平拉力F=(M+m)(a+μ1g)="135N" ②
（3）当F=120N时，铁箱与木块水平方向仍然一起加速，所以撤去拉力F时，箱和木块的速度均为v="6m/s," -③
因μ1>μ2, 以后木块相对箱滑动，木块加速度a2=μ2g=2.5m/s2- -④
又铁箱加速度：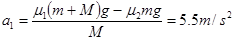
⑤
铁箱减速时间为t0=v/a1=1.1s>1s,故木块到达箱右端时，箱未能停止。 -⑥
则经t=1s木块比铁箱向右多移动距离L即铁箱长。
即有：L=(vt－a2t2/2)－(vt－a1t2/2) =(a1－a2)t2/2 ⑦
解得：L="1.5m-" ⑧
考点：本题主要考查了牛顿第二定律的直接应用，
点评：注意整理法和隔离法在题目中的应用，难度适中．
质量为M=2.5kg的一只长方体形铁箱在水平拉力F作用下沿水平面向右匀加速运动，铁箱与水平面间的动摩擦因数为μ1=0.50．这时铁箱内一个质量为m=0.5kg的木块恰好能静止在后壁上（如图所示），木块与铁箱内壁间的动摩擦因数为μ2=0.25．设最大静摩擦力等于滑动摩擦力，取g=10m/s2．求：
物体的质量为m=2.5kg，静止在水平地面上．物体跟地面间动摩擦因数μ=0.2，物体受到跟地面平行的拉力F作用，F大小随时间变化规律如图所示，F的方向不变，那么下述判断正确的是（g取10m/s2）（ ）
如图甲所示，水平平台的右端安装有轻质滑轮，质量为M=2.5kg的物块A放在与滑轮相距l的平台上，现有一轻绳跨过定滑轮，左端与物块连接，右端挂质量为m=0.5kg的小球B，绳拉直时用手托住小球使其在距地面h高处静止，绳与滑轮间的摩擦不计，重力加速度为g（g取10 m/s2）．设最大静摩擦力等于滑动摩擦力．
质量为M=2.5kg的一只长方体形铁箱在水平拉力F作用下沿水平面向右匀加速运动，铁箱与水平面间的动摩擦因数为μ1=0.50．这时铁箱内一个质量为m=0.5kg的木块恰好能静止在后壁上（如图所示），木块与铁箱内壁间的动摩擦因数为μ2=0.25．设最大静摩擦力等于滑动摩擦力，取g=10m/s2．求：
质量为M=2.5kg的一只长方体形状的铁箱在水平拉力F作用下沿水平面向右匀加速运动，铁箱与水平面间的动摩擦因数为μ1=0.50．这时铁箱内一个质量为m=0.5kg的木块恰好能静止在后壁上（如图所示），木块与铁箱内壁间的动摩擦因数为μ2=0.25．设最大静摩擦力等于滑动摩擦力，g取10m/s2．求：