题目内容
如图所示，在平行纸面内建立一个XOY平面直角坐标系，在此坐标系的第一象限内有垂直纸面向里的匀强磁场，磁感强度为B．一个质子和一个α粒子从坐标原点O垂直磁场方向以相同速度v进入磁场中，速度方向与磁场边界x轴夹角为
．已知质子的质量为m，带电荷量为e，α粒子的质量为4m，带电荷量为2e．
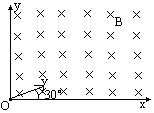
(1)质子与α粒子在磁场中运动时间之比为多少？
(2)分别求出这两个粒子射出磁场区域时的位置坐标．
答案：
解析：
解析：
|
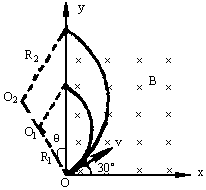
解：(1)带电粒子在洛伦兹力作用下做匀速圆周运动，根据牛顿第二定律得 qvB＝m 得带电粒子做圆周运动的周期 T＝ 根据左手定则判断，质子和α粒子均从y轴离开磁场，两种粒子在磁场转过的圆弧所对的圆心角相等，如答图所示．因此它们在磁场中的运动时间之比
将 mH＝m， (2)对于质子，根据牛顿第二定律可以得圆周运动的半径为 R＝ yH＝2RHcosθ＝ 同理，α粒子离开磁场的位置在y轴的坐标为 代入数据得 即质子和α粒子离开磁场时的位置坐标分别为： (0， |
， 而 T＝
，
，
等于它们运动的周期之比
，即
＝
＝
＝4m，qH＝e，
＝2e代入，得tH∶
＝1∶2． ②
由答图中的几何关系，质子做圆周运动的圆心O1与坐标原点的连线OO1与y轴的夹角θ＝
，则可得质子离开磁场的位置在y轴的坐标为
RH，得yH＝
③
＝2
cosθ＝
②
)；(0，
) ①
练习册系列答案
相关题目
（2013?开封一模）如图所示，在垂直纸面向里、磁感应强度为B的匀强磁场区域中，有一个均匀导线制成的单匝直角三角形线框，现用外力使线框以恒定的速度v沿垂直磁场方向向右运动，运动中线框的AB边始终与磁场右边界平行．已知AB=BC=l，线框导线的总电阻为R，则线框离开磁场的过程中（ ）
如图所示，在平行竖直虚线a与b、b与c、c与d之间分别存在着垂直于虚线的匀强电场、平行于虚线的匀强电场、垂直纸面向里的匀强磁场，虚线d处有一荧光屏．大量正离子（初速度和重力均忽略不计）从虚线a上的P孔处进入左边电场，经过三个场区后有一部分打在荧光屏上．关于这部分离子，若比荷| q |
| m |
| A、经过虚线c的位置越低 |
| B、经过虚线c的速度越大 |
| C、打在荧光屏上的位置越低 |
| D、打在荧光屏上的位置越高 |
如图所示，在平行于纸面的平面上建立一个xoy平面直角坐标系，在此坐标系的第一象限内有垂直纸面向里的匀强磁场，磁感应强度为B．一个反质子（质量与质子相同，电荷与质子等值反性）和一个．粒子从坐标原点0垂直磁场方向以相同速度v进入磁场中，速度方向与x轴夹角为30°．已知，反质子的质量为m，带电量为e且为负电荷，a粒子的质量为4m，带电量为2e．
如图所示，在平行带电金属板间有垂直于纸面向里的匀强磁场，质子、氘核、氚核沿平行于金属板方向，以相同动能射入两极板间，其中氘核沿直线运动，未发生偏转，质子和氚核发生偏转后射出，则：①偏向正极板的是质子；②偏向正极板的是氚核；③射出时动能最大的是质子；④射出时动能最大的是氚核．以上说法正确的是（ ）