题目内容
7. 如图所示,两水平平行导轨a、b相距L,a、b间有磁感应强度为B1的匀强磁场,磁场方向垂直导轨平面向上,a、b左端连接一电容为C、电压为U的电容器,右端有一与a、b垂直放置、质量为m的直导体棒,a,b导轨光滑,平行导轨c、d固定在水平面上,c,d相距为L,与水平面间的夹角为α,c、d导轨底端连接一阻值为R的电阻,磁感应强度为B2的匀强磁场垂直于c、d平面向上.将开关S闭合,棒由静止水平抛出,恰好从c,d导轨上端开始,沿c,d导轨做匀速运动,已知棒与c、d导轨间的动摩擦因数为μ,不计棒的电阻,重力加速度为g,求:
如图所示,两水平平行导轨a、b相距L,a、b间有磁感应强度为B1的匀强磁场,磁场方向垂直导轨平面向上,a、b左端连接一电容为C、电压为U的电容器,右端有一与a、b垂直放置、质量为m的直导体棒,a,b导轨光滑,平行导轨c、d固定在水平面上,c,d相距为L,与水平面间的夹角为α,c、d导轨底端连接一阻值为R的电阻,磁感应强度为B2的匀强磁场垂直于c、d平面向上.将开关S闭合,棒由静止水平抛出,恰好从c,d导轨上端开始,沿c,d导轨做匀速运动,已知棒与c、d导轨间的动摩擦因数为μ,不计棒的电阻,重力加速度为g,求:(1)棒沿c,d导轨运动的速度;
(2)棒抛出后,电容器的电压.
分析 (1)根据法拉第电磁感应定律和闭合电路的欧姆定律结合平衡条件求解速度大小;
(2)求出导体棒平抛出去瞬间的初速度大小,根据动量定理求解通过导体棒的电荷量,再根据电容的计算公式求解棒抛出后,电容器的电压.
解答 解:(1)棒沿c,d导轨做匀速运动时受力平衡,则有:
B2IL+μmgcosα=mgsinα,
根据法拉第电磁感应定律和闭合电路的欧姆定律可得:
I=$\frac{{B}_{2}Lv}{R}$,
联立解得:v=$\frac{mgR(sinα-μcosα)}{{B}_{2}^{2}{L}^{2}}$;
(2)导体棒平抛出去瞬间的初速度大小为:
v0=vcosα=$\frac{mgR(sinα-μcosα)cosα}{{B}_{2}^{2}{L}^{2}}$,
以导体棒为研究对象,根据动量定理可得:
${B}_{1}\overline{I}L•△t=m{v}_{0}-0$,
此过程通过导体棒的电荷量为:
q=$\overline{I}•△t$=$\frac{{m}^{2}gR(sinα-μcosα)cosα}{{{B}_{1}B}_{2}^{2}{L}^{3}}$,
电容器中剩余的电荷量为:
Q′=CU-q=CU-$\frac{{m}^{2}gR(sinα-μcosα)cosα}{{{B}_{1}B}_{2}^{2}{L}^{3}}$,
棒抛出后,电容器的电压为:
U′=$\frac{Q′}{C}$=U-$\frac{{m}^{2}gR(sinα-μcosα)cosα}{{{CB}_{1}B}_{2}^{2}{L}^{3}}$.
答:(1)棒沿c,d导轨运动的速度为$\frac{mgR(sinα-μcosα)}{{B}_{2}^{2}{L}^{2}}$;
(2)棒抛出后,电容器的电压为U-$\frac{{m}^{2}gR(sinα-μcosα)cosα}{{{CB}_{1}B}_{2}^{2}{L}^{3}}$.
点评 对于电磁感应问题研究思路常常有两条:一条从力的角度,重点是分析安培力作用下导体棒的平衡问题,根据平衡条件列出方程;另一条是能量,分析涉及电磁感应现象中的能量转化问题,根据动能定理、功能关系等列方程求解.

| A. | 力 路程 | B. | 质量 位移 | C. | 时间 质量 | D. | 位移 力 |
 航母飞行甲板前端上翘,水平部分与上翘部分通过一段圆弧平滑连接,D为圆弧最低点,圆弧半径为R.飞机以速度v越过D点时( )
航母飞行甲板前端上翘,水平部分与上翘部分通过一段圆弧平滑连接,D为圆弧最低点,圆弧半径为R.飞机以速度v越过D点时( )| A. | R越大,v越大,飞机起落架承受的作用力越小 | |
| B. | R越大,v越小,飞机起落架承受的作用力越大 | |
| C. | R越小,v越大,飞机起落架承受的作用力越大 | |
| D. | R越小,v越小,飞机起落架承受的作用力越小 |
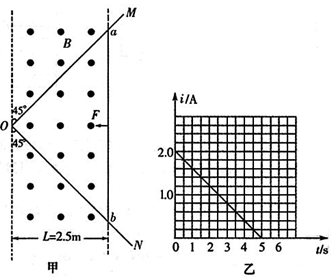 如图甲所示,垂直于水平桌面向上的有界匀强磁场的磁感应强度大小B=0.8T,宽度L=2.5m.光滑金属导轨OM、ON固定在桌面上,O点位于磁场的左边界,且OM、ON与磁场左边界均成45°角.金属棒ab放在导轨上,且与磁场的右边界重合.t=0时,ab棒在水平向左的外力F作用下向左运动并匀速通过磁场.测得回路中的感应电流I随时间t变化的图象如图乙所示.已知O点处电阻为R,其余电阻不计,则下列说法中正确的是( )
如图甲所示,垂直于水平桌面向上的有界匀强磁场的磁感应强度大小B=0.8T,宽度L=2.5m.光滑金属导轨OM、ON固定在桌面上,O点位于磁场的左边界,且OM、ON与磁场左边界均成45°角.金属棒ab放在导轨上,且与磁场的右边界重合.t=0时,ab棒在水平向左的外力F作用下向左运动并匀速通过磁场.测得回路中的感应电流I随时间t变化的图象如图乙所示.已知O点处电阻为R,其余电阻不计,则下列说法中正确的是( )| A. | 由图乙可知0~5s内通过ab棒横截面的电荷量为10C | |
| B. | 水平外力F随时间t变化的表达式为F=2(2-0.4t)2(N) | |
| C. | O点处的电阻为1Ω | |
| D. | 在0~5s内水平外力F做功的功率最大值为4W |
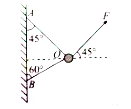 细线OA、OB的O端与质量为m的小球拴接在一起,A、B两端固定于墙面上同一竖直线上的两点,其中细线AO与竖直方向成45°角,细线BO与竖直方向成60°角.如图所示,现在对小球施加以个与水平方向成45°角的拉力F,小球保持静止,细线0A、OB均处于伸直状态,已知重力加速度为g,小球可视为质点.下列说法错误的是( )
细线OA、OB的O端与质量为m的小球拴接在一起,A、B两端固定于墙面上同一竖直线上的两点,其中细线AO与竖直方向成45°角,细线BO与竖直方向成60°角.如图所示,现在对小球施加以个与水平方向成45°角的拉力F,小球保持静止,细线0A、OB均处于伸直状态,已知重力加速度为g,小球可视为质点.下列说法错误的是( )| A. | 在保证细线OA、OB都伸直的情况下,若F增大,则细线OA中拉力减小,细线OB中拉力变大 | |
| B. | 当F=$\frac{\sqrt{2}}{2}$mg时,细线OB中拉力为0 | |
| C. | 为保证两根细线均伸直,拉力F不能超过$\frac{3\sqrt{2}+\sqrt{6}}{2}$mg | |
| D. | 若缓慢增大F且使小球始终处于平衡状态,则细线OA会松弛,细线OB将与F共线 |
| A. | 玻尔认为卢瑟福理论中电子绕核旋转的向心力来自库仑力是错误的,所以提出新的玻尔理论 | |
| B. | 卢瑟福得出原子核的体积极小的依据是绝大多数α粒子穿过金箔后仍按原来的方向前进 | |
| C. | 康普效应和光的双缝干涉实验都说明光具有粒子性 | |
| D. | 爱因斯坦用于解释光电效应的光子说依据的也是量子理论,所以光子说是在玻尔理论上发展的 |
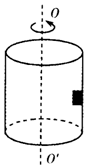 如图所示,在绕中心轴OO′的圆筒内壁上,有一物体随圆筒一起转动,在圆筒的角速度逐渐增大的过程中,物体相对圆筒始终未滑动,下列说法中正确的是( )
如图所示,在绕中心轴OO′的圆筒内壁上,有一物体随圆筒一起转动,在圆筒的角速度逐渐增大的过程中,物体相对圆筒始终未滑动,下列说法中正确的是( )| A. | 物体所受弹力逐渐增大,摩擦力大小一定不变 | |
| B. | 物体所受弹力不变,摩擦力大小减小了 | |
| C. | 物体所受的摩擦力与竖直方向的夹角不为零 | |
| D. | 物体所受弹力提供向心力改变速度的方向并且在逐渐增大,静摩擦力的竖直分力平衡重力,水平分力使速度大小增大 |
 在磁感应强度为B=2T的匀强磁场中,有一个半径r=0.5m的金属圆环,圆环所在的平面与磁感线垂直,OA是一个金属棒,它沿顺时针方向以ω=12rad/s的角速度绕围心O匀速转动,A端始终与圆环相接触,OA棒的电阻R=0.1Ω,图中定值电阻R1=5Ω,R2=20Ω,电压表理想电压表,圆环和导线的电阻忽略不计,求:
在磁感应强度为B=2T的匀强磁场中,有一个半径r=0.5m的金属圆环,圆环所在的平面与磁感线垂直,OA是一个金属棒,它沿顺时针方向以ω=12rad/s的角速度绕围心O匀速转动,A端始终与圆环相接触,OA棒的电阻R=0.1Ω,图中定值电阻R1=5Ω,R2=20Ω,电压表理想电压表,圆环和导线的电阻忽略不计,求: 如图所示为一半球形玻璃砖,其直径为MN,将玻璃砖按图中的方式放置,此时直径MN呈竖直状态,其中O点为玻璃砖的球心,一细光速沿与MN平行的方向向下射向半球形玻璃砖的某位置S点,经玻璃砖折射后刚好从N点射出,已知玻璃砖的半径为2m,玻璃砖的折射率为n=$\sqrt{3}$,求入射点S到直径MN的距离.
如图所示为一半球形玻璃砖,其直径为MN,将玻璃砖按图中的方式放置,此时直径MN呈竖直状态,其中O点为玻璃砖的球心,一细光速沿与MN平行的方向向下射向半球形玻璃砖的某位置S点,经玻璃砖折射后刚好从N点射出,已知玻璃砖的半径为2m,玻璃砖的折射率为n=$\sqrt{3}$,求入射点S到直径MN的距离.