题目内容
如图所示,物块A以12m/s的初速度从P点开始在长12m的平直轨道上运动,在A前进方向上某位置放一物块B,A碰上B后立即与B粘在一起共同向前运动,A、B与轨道之间的动摩擦因数均为0.2,A与B的质量之比为1:2,A、B两物块可视为质点,为使A、B刚好停在轨道末端,求物块B碰前的位置.(g取10m/s2)


分析:A碰上B前的过程,根据动能定理列出等式求出A碰上B前的速度,
根据动量守恒求出A碰上B后立即与B粘在一起共同向前的速度,再运用动能定理研究共同向前运动的过程求解.
根据动量守恒求出A碰上B后立即与B粘在一起共同向前的速度,再运用动能定理研究共同向前运动的过程求解.
解答:解:设A与B的质量分别是m、2m,A碰上B前的速度为v1,受到摩擦力为umg,
A碰上B后立即与B粘在一起共同向前运动的速度为v2,物块B碰前的位置离A初始位置xm.
A碰上B前的过程,根据动能定理得:
-umgx=
m
-
m
… ①
A碰上B的过程,根据动量守恒得:
mv1=(m+2m)v2…②
A碰上B后立即与B粘在一起共同向前运动的过程,利用动能定理得:
-u×3mgx=0-
×3m
联立①②③解得:x=9m
答:物块B碰前的位置离A初始位置9 m.
A碰上B后立即与B粘在一起共同向前运动的速度为v2,物块B碰前的位置离A初始位置xm.
A碰上B前的过程,根据动能定理得:
-umgx=
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 0 |
A碰上B的过程,根据动量守恒得:
mv1=(m+2m)v2…②
A碰上B后立即与B粘在一起共同向前运动的过程,利用动能定理得:
-u×3mgx=0-
| 1 |
| 2 |
| v | 2 2 |
联立①②③解得:x=9m
答:物块B碰前的位置离A初始位置9 m.
点评:本题考查了动量守恒定律、动能定理等知识,综合性较强,关键是理清运动过程,选择合适的规律进行求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,物块A、木板B的质量均为m=10kg,不计A的大小,B板长L=3m.开始时A、B均静止.现给A以2m/s的水平向右的初速度从B的左端开始运动,同时给A施加一个F=30N的水平向右的外力.已知A与B、B与地面之间的动摩擦因数分别为μ1=0.3和μ2=0.1.g取10m/s2.
如图所示,物块A、木板B的质量均为m=10kg,不计A的大小,B板长L=3m.开始时A、B均静止.现给A以2m/s的水平向右的初速度从B的左端开始运动,同时给A施加一个F=30N的水平向右的外力.已知A与B、B与地面之间的动摩擦因数分别为μ1=0.3和μ2=0.1.g取10m/s2.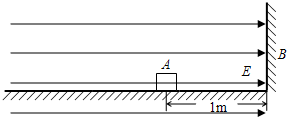 如图所示,物块A(可视为质点)的质量为1.0×10-2kg,带1.0×10-8C的正电荷.A与水平桌面间的动摩擦因数为μ=0.2,B为竖直挡板,A与挡板相距1.0m.A以6m/s的速度向B运动,在A运动的空间里存在着水平向右的匀强电场,场强E=8.0×106N/C.设A与B相碰无机械能损失,A在运动中电量不变.求物块A从图示位置开始到最后停止的过程中
如图所示,物块A(可视为质点)的质量为1.0×10-2kg,带1.0×10-8C的正电荷.A与水平桌面间的动摩擦因数为μ=0.2,B为竖直挡板,A与挡板相距1.0m.A以6m/s的速度向B运动,在A运动的空间里存在着水平向右的匀强电场,场强E=8.0×106N/C.设A与B相碰无机械能损失,A在运动中电量不变.求物块A从图示位置开始到最后停止的过程中 如图所示,物块A的质量为10克,带10-8库的正电荷,A与水平桌面间的动摩擦因数为0.1,B为竖直挡板,A与挡板相距1米.现A以4米/秒的速度向B运动,在A运动的空间里存在着水平向右的匀强电场,场强E=3×106牛/库.设A与B相碰无机械能损失,A在运动中电量不变.求物块A从图示位置开始,到最后停止的过程中,距B板最大距离及通过的总路程.
如图所示,物块A的质量为10克,带10-8库的正电荷,A与水平桌面间的动摩擦因数为0.1,B为竖直挡板,A与挡板相距1米.现A以4米/秒的速度向B运动,在A运动的空间里存在着水平向右的匀强电场,场强E=3×106牛/库.设A与B相碰无机械能损失,A在运动中电量不变.求物块A从图示位置开始,到最后停止的过程中,距B板最大距离及通过的总路程. 如图所示,物块A、木板B的质量均为m=10kg,不计A的大小,B板长3m.开始时A、B均静止.现给A以2m/s的水平初速度从B的最左端开始运动,为了维持A的速度始终不变,在A获得初速度的同时给A施加一水平外力F作用.已知A与B、B与地之间的动摩擦因数分别为μ1=0.3和μ2=0.1.g取10m/s2.
如图所示,物块A、木板B的质量均为m=10kg,不计A的大小,B板长3m.开始时A、B均静止.现给A以2m/s的水平初速度从B的最左端开始运动,为了维持A的速度始终不变,在A获得初速度的同时给A施加一水平外力F作用.已知A与B、B与地之间的动摩擦因数分别为μ1=0.3和μ2=0.1.g取10m/s2.