题目内容
2. 空间存在正交的电、磁场(电场强度方向水平向左、大小为E,磁感应强度方向垂直纸面向内、大小为B),场中竖直固定一根绝缘直棒,一个质量为m、带电荷量为q的小球套在棒上沿棒滑动,小球与棒间的动摩擦因数为μ,且$\frac{mg}{2}$<μqE<mg.现将小球由静止释放.
空间存在正交的电、磁场(电场强度方向水平向左、大小为E,磁感应强度方向垂直纸面向内、大小为B),场中竖直固定一根绝缘直棒,一个质量为m、带电荷量为q的小球套在棒上沿棒滑动,小球与棒间的动摩擦因数为μ,且$\frac{mg}{2}$<μqE<mg.现将小球由静止释放.(1)试分析小球的运动情况;
(2)求小球的最大加速度am;
(3)求当小球的加速度大小为$\frac{1}{2}$am时小球的速度.
分析 (1、2)小球受重力、摩擦力(可能有)、弹力(可能有)、向右的洛伦兹力、向左的电场力,当洛伦兹力等于电场力时,合力等于重力,加速度最大;
当洛伦兹力大于电场力,且滑动摩擦力与重力平衡时,速度最大,从而确定小球运动情况.
(3)对小球进行受力分析,依据牛顿第二定律,即可求解加速度大小为$\frac{1}{2}$am时小球的速度,注意有两种情况.
解答 解:(1)小球受重力、摩擦力(可能有)、弹力(可能有)、向左的洛伦兹力、向右的电场力,
当洛伦兹力等于电场力时,合力等于重力,加速度最大,
当洛伦兹力大于电场力,且滑动摩擦力与重力平衡时,速度最大,
那么小球先做加速度增大的加速运动,再做加速度减小的加速度,最后做匀速直线运动;
(2)由上分析,则有:
mg=mamax;
qE=qvB
解得:amax=g;
(3)当洛仑兹力等于电场力时,摩擦力为零,此时加速度为g,达最大;此后速度继续增大,则洛仑兹力增大,水平方向上的合力增大,摩擦力将增大;加速度将减小,故最大加速度的一半会有两种情况,一是在洛仑兹力小于电场力的时间内,另一种是在洛仑兹力大于电场力的情况下,
则:$\frac{g}{2}$=$\frac{mg-μ(qE-Bq{v}_{1})}{m}$,
解得:v1=$\frac{2μqE-mg}{2μqB}$;
当洛伦兹力大于电场力时,则有:$\frac{g}{2}$=$\frac{mg-μ(Bq{v}_{2}-qE)}{m}$,
解得:v2=$\frac{2μqE+mg}{2μqB}$;
答:(1)小球先做加速度增大的加速运动,再做加速度减小的加速度,最后做匀速直线运动;
(2)小球的最大加速度g;
(3)当小球的加速度大小为$\frac{1}{2}$am时小球的速度分别为$\frac{2μqE-mg}{2μqB}$ 与$\frac{2μqE+mg}{2μqB}$.
点评 本题要注意分析带电小球的运动过程,属于牛顿第二定律的动态应用与电磁场结合的题目,此类问题要求能准确找出物体的运动过程,并能分析各力的变化,对学生要求较高.

 口算能手系列答案
口算能手系列答案
| A. | 0.02s,314V | B. | 0.01s,314V | C. | 0.02s,220V | D. | 0.01s,220V |

| A. | 振荡电流i在增大 | B. | 电容器正在放电 | ||
| C. | 电容器中的电场强度正在增大 | D. | 电场能正在向磁场能转化 |
 游乐园里小明在玩套圈游戏,他想用一个竹圈套住离他x=5m远的一个小玩偶,如图所示,水平抛出竹圈时手的高度约为1.25m,不考虑空气阻力,g取10m/s2,求:
游乐园里小明在玩套圈游戏,他想用一个竹圈套住离他x=5m远的一个小玩偶,如图所示,水平抛出竹圈时手的高度约为1.25m,不考虑空气阻力,g取10m/s2,求: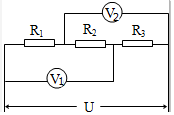 如图所示电路中定值电阻R1=5Ω,R3=20Ω,把它们与R2串联后接在电压为U的稳压电源上时.电压表V1的示数为10V,V2示数为25V,则R2的阻值和电源电压U的值分别为多少?
如图所示电路中定值电阻R1=5Ω,R3=20Ω,把它们与R2串联后接在电压为U的稳压电源上时.电压表V1的示数为10V,V2示数为25V,则R2的阻值和电源电压U的值分别为多少?
 如图是一种腹部先着水的跳水比赛,击水时水花最大者获胜,水花的大小主要取决于运动员入水时具有的动能.假设甲、乙运动员都站在3m高的平台上(甲、乙站立时的重心位置离平台均为1m),其中质量为120kg的甲简单的步出平台倒向水面,若质量为100kg的乙要想不输于甲,则需通过起跳使自身重心至少升高约( )
如图是一种腹部先着水的跳水比赛,击水时水花最大者获胜,水花的大小主要取决于运动员入水时具有的动能.假设甲、乙运动员都站在3m高的平台上(甲、乙站立时的重心位置离平台均为1m),其中质量为120kg的甲简单的步出平台倒向水面,若质量为100kg的乙要想不输于甲,则需通过起跳使自身重心至少升高约( ) 如图所示,一个质量为m=0.03kg,带电量为q=-1.0×10-8C的带电小球,用绝缘细线悬挂在某水平方向的匀强电场中,图中实线为电场线.当小球静止时,测得悬线与竖直方向成30°角.(取g=10m/s2 )
如图所示,一个质量为m=0.03kg,带电量为q=-1.0×10-8C的带电小球,用绝缘细线悬挂在某水平方向的匀强电场中,图中实线为电场线.当小球静止时,测得悬线与竖直方向成30°角.(取g=10m/s2 )