题目内容
一质量为m=4kg的玩具车,以恒定功率p0在平直路面上加速行驶,t=10s内走过s=14m,且小车由初速度v1=1m/s增大到最大速度v2=2m/s,行驶中小车受到的阻力f恒定,则:
(1)玩具车阻力f表达式是什么?
(2)玩具车这段时间内牵引力做的功的表达式的什么?
(3)由止求出玩具车的额定功率p0为多大?
(1)玩具车阻力f表达式是什么?
(2)玩具车这段时间内牵引力做的功的表达式的什么?
(3)由止求出玩具车的额定功率p0为多大?
分析:(1)玩具车受到的阻力等于最大速度时的牵引力.
(2)因为玩具车是以恒定功率启动的,所以牵引力做的功W=Pt.
(3)在整个运动过程中由动能定理可求出额定功率.
(2)因为玩具车是以恒定功率启动的,所以牵引力做的功W=Pt.
(3)在整个运动过程中由动能定理可求出额定功率.
解答:解:(1)当速度达到最大时,牵引力等于阻力由P0=Fv2=fv2得:
f=
(2)玩具车以恒定的功率启动,所以牵引力做功为
WF=p0t
(3)在整个运动过程中由动能定理有:
p0t-fs=
m
-
m
f=
联立以上两式解得p0t-
s=
m
-
m
P0=
=
W=2W
答:(1)玩具车阻力f表达式是f=
.
(2)玩具车这段时间内牵引力做的功的表达式WF=p0t.
(3)由止求出玩具车的额定功率p0为2W.
f=
| p0 |
| v2 |
(2)玩具车以恒定的功率启动,所以牵引力做功为
WF=p0t
(3)在整个运动过程中由动能定理有:
p0t-fs=
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| v | 2 1 |
f=
| P0 |
| V2 |
联立以上两式解得p0t-
| p0 |
| V2 |
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| v | 2 1 |
P0=
| ||||
t-
|
| ||
10-
|
答:(1)玩具车阻力f表达式是f=
| p0 |
| v2 |
(2)玩具车这段时间内牵引力做的功的表达式WF=p0t.
(3)由止求出玩具车的额定功率p0为2W.
点评:本题中汽车以恒定功率启动,当牵引力等于阻力时,速度达到最大,关键要灵活选择研究的过程,运用动能定理求解.

练习册系列答案
相关题目
 水平传送带被广泛地应用于机场和火车站,如图所示为一水平传送带装置示意图.紧绷的传送带AB始终保持恒定的速率v=1m/s运行,一质量为m=4kg的行李无初速度地放在A处,传送带对行李的滑动摩擦力使行李开始做匀加速直线运动,随后行李又以与传送带相等的速率做匀速直线运动.设行李与传送带之间的动摩擦因数μ=0.1,A、B间的距离L=2m,g取10m/s2.求:
水平传送带被广泛地应用于机场和火车站,如图所示为一水平传送带装置示意图.紧绷的传送带AB始终保持恒定的速率v=1m/s运行,一质量为m=4kg的行李无初速度地放在A处,传送带对行李的滑动摩擦力使行李开始做匀加速直线运动,随后行李又以与传送带相等的速率做匀速直线运动.设行李与传送带之间的动摩擦因数μ=0.1,A、B间的距离L=2m,g取10m/s2.求: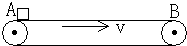 水平传送带被广泛地应用于机场和火车站,用于对旅客的行李进行了安全检查.右图为一水平传送带装置示意图,绷紧的传送带AB始终保持v=1m/s的恒定速率运行,一质量为m=4kg的行李无初速地放在A处,传送带对行李的滑动摩擦力使行李开始做匀加速直线运动,随后行李又以与传送带相等的速率做匀速直线运动.设行李与传送带间的动摩擦因数μ=0.1,AB间的距离L=2m,g取10m/s2.求:
水平传送带被广泛地应用于机场和火车站,用于对旅客的行李进行了安全检查.右图为一水平传送带装置示意图,绷紧的传送带AB始终保持v=1m/s的恒定速率运行,一质量为m=4kg的行李无初速地放在A处,传送带对行李的滑动摩擦力使行李开始做匀加速直线运动,随后行李又以与传送带相等的速率做匀速直线运动.设行李与传送带间的动摩擦因数μ=0.1,AB间的距离L=2m,g取10m/s2.求: 如图所示,在水平地面上有一个长L=1.5m,高h=0.8m的长方体木箱,其质量为M=1kg,与地面的动摩擦因数μ=0.3.在它的上表面的左端放有一质量为m=4kg的小铁块,铁块与木箱的摩擦不计.开始它们均静止.现对木箱施加一水平向左的恒力F=27N.(g=10m/s2)问:
如图所示,在水平地面上有一个长L=1.5m,高h=0.8m的长方体木箱,其质量为M=1kg,与地面的动摩擦因数μ=0.3.在它的上表面的左端放有一质量为m=4kg的小铁块,铁块与木箱的摩擦不计.开始它们均静止.现对木箱施加一水平向左的恒力F=27N.(g=10m/s2)问: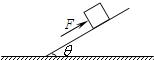 如图,一质量为m=4kg的物体放在一倾角为θ=370的斜面上,当用一沿斜面向上的力F=30.4N推它时,恰能沿斜面向上作匀速直线运动,求
如图,一质量为m=4kg的物体放在一倾角为θ=370的斜面上,当用一沿斜面向上的力F=30.4N推它时,恰能沿斜面向上作匀速直线运动,求