题目内容
19. 1931年英国物理学家狄拉克从理论上预言:存在只有一个磁极的粒子,即“磁单极子”.假设一个“N磁单极子”形成的磁场如图所示,将一个半径为r、质量为m的超导体圆环水平放置在该磁单极子的正上方,圆环所在位置的磁感应强度大小为B,与圆环相切的磁感线与竖直方向的夹角为30°,重力加速度大小为g,若圆环恰好在该位置悬浮,则圆环中电流的大小为( )
1931年英国物理学家狄拉克从理论上预言:存在只有一个磁极的粒子,即“磁单极子”.假设一个“N磁单极子”形成的磁场如图所示,将一个半径为r、质量为m的超导体圆环水平放置在该磁单极子的正上方,圆环所在位置的磁感应强度大小为B,与圆环相切的磁感线与竖直方向的夹角为30°,重力加速度大小为g,若圆环恰好在该位置悬浮,则圆环中电流的大小为( )| A. | $\frac{mg}{2πrB}$ | B. | $\frac{mg}{πrB}$ | C. | $\frac{\sqrt{3}mg}{2πrB}$ | D. | $\frac{\sqrt{3}mg}{πrB}$ |
分析 将圆环等效为许多很短的电流元组成,每段电流元都受到安培力,因为圆环平衡,安培力的合力竖直向上与重力平衡,由左手受定则知电流逆时针方向.
解答  将磁感应强度B沿水平和竖直方向进行正交分解,如图${B}_{1}^{\;}=Bsin30°=\frac{B}{2}$;${B}_{2}^{\;}=Bcos30°=\frac{\sqrt{3}}{2}B$
将磁感应强度B沿水平和竖直方向进行正交分解,如图${B}_{1}^{\;}=Bsin30°=\frac{B}{2}$;${B}_{2}^{\;}=Bcos30°=\frac{\sqrt{3}}{2}B$
利用微元法思想,把圆环分割成许多极短的电流元,根据左手定则,每小段电流元所受的磁场竖直分量的作用力沿半径方向向外,根据对称性,沿半径方向安培力合力为零
磁场的水平分量产生的安培力竖直向上$F={B}_{1}^{\;}IL=\frac{B}{2}I(2πr)=πBIr$
F=mg即BπIr=mg
解得$I=\frac{mg}{πrB}$
故选:B
点评 本题解题的列式的依据是共点力的平衡,要注意磁感应强度是矢量,分解遵循平行四边形定则.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
9.如图1是演示简谐运动图象的装置,当盛沙漏斗下面的薄木板N被匀速地拉出时,摆动着的漏斗中漏出的沙在板上形成的曲线显示出摆的位移随时间变化的关系,板上直线OO′代表时间轴.图2是一次实验中用同一个摆长不变的摆做出的两组操作形成的曲线,若板N1和N2拉动速度用v1和v2表示,板N1和N2上曲线所代表的摆动周期用T1和T2表示,则( )
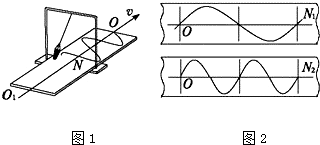

| A. | T1=2T2 | B. | 2T1=T2 | C. | v1=2v2 | D. | 2v1=v2 |
10.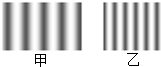 图甲、图乙为两次用单色光做双缝干涉实验时,屏幕上显示的图样.图甲条纹间距明显大于图乙,比较两次实验( )
图甲、图乙为两次用单色光做双缝干涉实验时,屏幕上显示的图样.图甲条纹间距明显大于图乙,比较两次实验( )
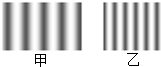 图甲、图乙为两次用单色光做双缝干涉实验时,屏幕上显示的图样.图甲条纹间距明显大于图乙,比较两次实验( )
图甲、图乙为两次用单色光做双缝干涉实验时,屏幕上显示的图样.图甲条纹间距明显大于图乙,比较两次实验( )| A. | 若光屏到双缝的距离相等,则图甲对应的波长较大 | |
| B. | 若光源、双缝间隙相同,则图甲光屏到双缝的距离较大 | |
| C. | 若光源、光屏到双缝的距离相同,则图甲双缝间隙较小 | |
| D. | 图甲的光更容易产生明显的衍射现象 |
7. a、b、c三个物体在同一条直线上运动,其位移与时间的关系图象中,图线c是一条x=0.4t2的抛物线.有关这三个物体在0~5s内的运动,下列说法正确的是( )
a、b、c三个物体在同一条直线上运动,其位移与时间的关系图象中,图线c是一条x=0.4t2的抛物线.有关这三个物体在0~5s内的运动,下列说法正确的是( )
 a、b、c三个物体在同一条直线上运动,其位移与时间的关系图象中,图线c是一条x=0.4t2的抛物线.有关这三个物体在0~5s内的运动,下列说法正确的是( )
a、b、c三个物体在同一条直线上运动,其位移与时间的关系图象中,图线c是一条x=0.4t2的抛物线.有关这三个物体在0~5s内的运动,下列说法正确的是( )| A. | a物体做匀加速直线运动 | |
| B. | c物体做匀加速直线运动 | |
| C. | t=5s时,a物体速度比c物体速度大 | |
| D. | a、b两物体都做匀速直线运动,且速度相同 |
14. 滑块a质量为5m,滑块b质量为m,一根水平直杆穿过两个滑块,如图所示.直杆可绕竖直轴OO′在水平面内转动,滑块a距转轴R.滑块b距转轴2R.两滑块用轻绳连接,最初轻绳伸直但并无张力.滑块与直杆间的最大静摩擦力为滑块重力的k倍,且最大静摩擦力与滑动摩擦力相等,重力加速度大小为g.如果直杆从静止开始绕转轴缓慢地加速转动,用ω表示其转动的角速度,下列说法正确的是( )
滑块a质量为5m,滑块b质量为m,一根水平直杆穿过两个滑块,如图所示.直杆可绕竖直轴OO′在水平面内转动,滑块a距转轴R.滑块b距转轴2R.两滑块用轻绳连接,最初轻绳伸直但并无张力.滑块与直杆间的最大静摩擦力为滑块重力的k倍,且最大静摩擦力与滑动摩擦力相等,重力加速度大小为g.如果直杆从静止开始绕转轴缓慢地加速转动,用ω表示其转动的角速度,下列说法正确的是( )
 滑块a质量为5m,滑块b质量为m,一根水平直杆穿过两个滑块,如图所示.直杆可绕竖直轴OO′在水平面内转动,滑块a距转轴R.滑块b距转轴2R.两滑块用轻绳连接,最初轻绳伸直但并无张力.滑块与直杆间的最大静摩擦力为滑块重力的k倍,且最大静摩擦力与滑动摩擦力相等,重力加速度大小为g.如果直杆从静止开始绕转轴缓慢地加速转动,用ω表示其转动的角速度,下列说法正确的是( )
滑块a质量为5m,滑块b质量为m,一根水平直杆穿过两个滑块,如图所示.直杆可绕竖直轴OO′在水平面内转动,滑块a距转轴R.滑块b距转轴2R.两滑块用轻绳连接,最初轻绳伸直但并无张力.滑块与直杆间的最大静摩擦力为滑块重力的k倍,且最大静摩擦力与滑动摩擦力相等,重力加速度大小为g.如果直杆从静止开始绕转轴缓慢地加速转动,用ω表示其转动的角速度,下列说法正确的是( )| A. | 轻绳张紧前a、b所受的摩擦力始终相等 | |
| B. | 如果去掉轻绳,b比a先开始滑动 | |
| C. | 轻绳刚开始张紧时,滑块a受到的摩擦力大小为2.5kmg | |
| D. | 当$ω=\sqrt{\frac{kg}{R}}$时,a所受摩擦力的大小为0 |
10.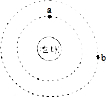 如图,若两颗人造卫星a和b均绕地球作匀速圆周运动,且a、b在运动过程中仅受地球万有引力的作用,a、b绕地球运动的线速度大小分别为v1、v2,周期分别为T1、T2,则( )
如图,若两颗人造卫星a和b均绕地球作匀速圆周运动,且a、b在运动过程中仅受地球万有引力的作用,a、b绕地球运动的线速度大小分别为v1、v2,周期分别为T1、T2,则( )
 如图,若两颗人造卫星a和b均绕地球作匀速圆周运动,且a、b在运动过程中仅受地球万有引力的作用,a、b绕地球运动的线速度大小分别为v1、v2,周期分别为T1、T2,则( )
如图,若两颗人造卫星a和b均绕地球作匀速圆周运动,且a、b在运动过程中仅受地球万有引力的作用,a、b绕地球运动的线速度大小分别为v1、v2,周期分别为T1、T2,则( )| A. | lg($\frac{{v}_{1}}{{v}_{2}}$)=$\frac{1}{3}$lg($\frac{{T}_{1}}{{T}_{2}}$) | B. | lg($\frac{{v}_{1}}{{v}_{2}}$)=3lg($\frac{{T}_{1}}{{T}_{2}}$) | ||
| C. | lg($\frac{{v}_{1}}{{v}_{2}}$)=$\frac{1}{3}$lg($\frac{{T}_{2}}{{T}_{1}}$) | D. | lg($\frac{{v}_{1}}{{v}_{2}}$)=3lg($\frac{{T}_{2}}{{T}_{1}}$) |
7.下面说法中,正确的是( )
| A. | 匀变速直线运动是速度不变的运动 | |
| B. | 匀变速直线运动是速度不断增加的直线运动 | |
| C. | 匀变速直线运动是加速度不变的直线运动 | |
| D. | 匀变速直线运动是加速度和速度都不变的运动 |

 太空中的物体处于完全失重状态,无法用天平直接测量其质量.为测定一小球的质量,将小球放在带有压力传感器的小车上,小车在电机带动下向右做匀加速运动,并通过速度传感器测出挡光片Ⅰ、挡光片Ⅱ经过速度传感器时的速度.通过计算机程序显示出小球的质量.
太空中的物体处于完全失重状态,无法用天平直接测量其质量.为测定一小球的质量,将小球放在带有压力传感器的小车上,小车在电机带动下向右做匀加速运动,并通过速度传感器测出挡光片Ⅰ、挡光片Ⅱ经过速度传感器时的速度.通过计算机程序显示出小球的质量.