题目内容
竖直平面内的圆环,O为圆心,A为最高点.将物体从A点释放经t1落到B点;沿光滑斜面CB物体从C点由静止释放经t2落到B点;沿光滑斜面DB将物体从D点由静止释放经t3落到B点.关于t1、t2、t3的大小,以下说法中正确的是( )
A.t1>t2>t3
B.t1=t2=t3
C.t1>t2=t3
D.以上答案均不正确
【答案】分析:先计算出每条轨道的加速度,在计算出每条路径的轨道,最后联立求得时间与轨道和竖直方向的夹角无关.
解答:解:设运动轨道与竖直方向的夹角为θ,圆环的半径为R,则轨道长度为2Rcosθ,物体的初速度为零,加速度为gcosθ,物体做匀加速直线运动,公式 ,s=2Rcosθ,所以时间
,s=2Rcosθ,所以时间 ,与角θ的大小无关.故B正确.
,与角θ的大小无关.故B正确.
故选:B.
点评:只要证明所用时间与轨道与竖直方向的夹角无关即可解决此类题目.
解答:解:设运动轨道与竖直方向的夹角为θ,圆环的半径为R,则轨道长度为2Rcosθ,物体的初速度为零,加速度为gcosθ,物体做匀加速直线运动,公式
 ,s=2Rcosθ,所以时间
,s=2Rcosθ,所以时间 ,与角θ的大小无关.故B正确.
,与角θ的大小无关.故B正确.故选:B.
点评:只要证明所用时间与轨道与竖直方向的夹角无关即可解决此类题目.

练习册系列答案
相关题目
 竖直平面内的圆环,O为圆心,A为最高点.将物体从A点释放经t1落到B点;沿光滑斜面CB物体从C点由静止释放经t2落到B点;沿光滑斜面DB将物体从D点由静止释放经t3落到B点.关于t1、t2、t3的大小,以下说法中正确的是( )
竖直平面内的圆环,O为圆心,A为最高点.将物体从A点释放经t1落到B点;沿光滑斜面CB物体从C点由静止释放经t2落到B点;沿光滑斜面DB将物体从D点由静止释放经t3落到B点.关于t1、t2、t3的大小,以下说法中正确的是( )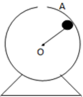 如图所示,小球(可被视作质点)质量为m,固定在竖直平面内的圆环其最高处有一小缺口A,小缺口的直径略大于小球的直径.细绳拉着小球在圆环内绕环心O做圆周运动,小球不脱离圆轨道,圆环半径为r,细绳的长度也是r.细绳所能承受的最大张力为小球重力的3倍.用g表示重力加速度.小球在最高点A允许的最大速率和最小速率是多大?
如图所示,小球(可被视作质点)质量为m,固定在竖直平面内的圆环其最高处有一小缺口A,小缺口的直径略大于小球的直径.细绳拉着小球在圆环内绕环心O做圆周运动,小球不脱离圆轨道,圆环半径为r,细绳的长度也是r.细绳所能承受的最大张力为小球重力的3倍.用g表示重力加速度.小球在最高点A允许的最大速率和最小速率是多大? 竖直平面内的圆环,O为圆心,A为最高点.将物体从A点释放经t1落到B点;沿光滑斜面CB物体从C点由静止释放经t2落到B点;沿光滑斜面DB将物体从D点由静止释放经t3落到B点.关于t1、t2、t3的大小,以下说法中正确的是
竖直平面内的圆环,O为圆心,A为最高点.将物体从A点释放经t1落到B点;沿光滑斜面CB物体从C点由静止释放经t2落到B点;沿光滑斜面DB将物体从D点由静止释放经t3落到B点.关于t1、t2、t3的大小,以下说法中正确的是