题目内容
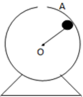如图所示，小球（可被视作质点）质量为m，固定在竖直平面内的圆环其最高处有一小缺口A，小缺口的直径略大于小球的直径．细绳拉着小球在圆环内绕环心O做圆周运动，小球不脱离圆轨道，圆环半径为r，细绳的长度也是r．细绳所能承受的最大张力为小球重力的3倍．用g表示重力加速度．小球在最高点A允许的最大速率和最小速率是多大？分析：在最高点，小球受重力和绳子的拉力，合力提供向心力；当拉力为零时速度最小，拉力为3mg时速度最大．
解答：解：在最高点，小球受重力和绳子的拉力，合力提供向心力；
当拉力为零时速度最小，根据牛顿第二定律，有：
mg=m
解得：vmin=
拉力为3mg时速度最大，根据牛顿第二定律，有：
3mg+mg=m
解得：vmax=2
答：小球在最高点A允许的最大速率为2
，最小速率是
．
当拉力为零时速度最小，根据牛顿第二定律，有：
mg=m
| vmin2 |
| r |
解得：vmin=
| gr |
拉力为3mg时速度最大，根据牛顿第二定律，有：
3mg+mg=m
| vmax2 |
| r |
解得：vmax=2
| gr |
答：小球在最高点A允许的最大速率为2
| gr |
| gr |
点评：本题关键是明确向心力来源，根据牛顿第二定律列式求解，注意临界状态的确定．
练习册系列答案
相关题目
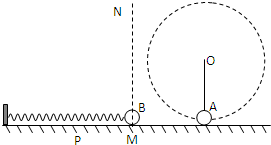如图所示，水平地面上方被竖直线MN分隔成两部分，M点左侧地面粗糙，与B球间的动摩擦因数为μ=0.5，右侧光滑．MN右侧空间有一范围足够大的匀强电场，在O点用长为R=5m的轻质绝缘细绳，拴一个质量mA=0.04kg，带电量为q=+2×10-4C的小球A，在竖直平面内以v=10m/s的速度做顺时针匀速圆周运动，小球A运动到最低点时与地面刚好不接触．处于原长的弹簧左端连在墙上，右端与不带电的小球B接触但不粘连，B球的质量mB=0.02kg，此时B球刚好位于M点．现用水平向左的推力将B球缓慢推至P点（弹簧仍在弹性限度内），MP之间的距离为L=10cm，推力所做的功是W=0.27J，当撤去推力后，B球沿地面向右滑动恰好能和A球在最低点处发生正碰，并瞬间成为一个整体C（A、B、C均可视为质点），速度大小变为5m/s，方向向左；碰撞前后电荷量保持不变，碰后瞬间立即把匀强电场的场强大小变为E=6×103N/C，电场方向不变，求：
（2009?丰台区一模）如图所示，水平地面上方被竖直线MN分隔成两部分，M点左侧地面粗糙，动摩擦因数为μ=0.5，右侧光滑．MN右侧空间有一范围足够大的匀强电场．在O点用长为R=5m的轻质绝缘细绳，拴一个质量mA=0.04kg，带电量为q=+2×10-4的小球A，在竖直平面内以v=10m/s的速度做顺时针匀速圆周运动，运动到最低点时与地面刚好不接触．处于原长的弹簧左端连在墙上，右端与不带电的小球B接触但不粘连，B球的质量mB=0.02kg，此时B球刚好位于M点．现用水平向左的推力将B球缓慢推至P点（弹簧仍在弹性限度内），MP之间的距离为L=10cm，推力所做的功是W=0.27J，当撤去推力后，B球沿地面右滑恰好能和A球在最低点处发生正碰，并瞬间成为一个整体C（A、B、C均可视为质点），碰后瞬间立即把匀强电场的场强大小变为E=6×103N/C，电场方向不变．（取g=10m/s2）求：
