题目内容
一平行板电容器，已知极板长度为L，板间距离为d，两极板间所加电压为U．一质量为m、电荷量为q的带电粒子（不计重力），沿两极板中线以某一初速度进入电场，恰好从极板边缘飞出．则根据上述已知量能够求得下列哪些物理量（ ）A．速度的偏转角
B．离开电场时的动能
C．离开电场时的电势能
D．在电场中的运动时间
【答案】分析：粒子在电场中做类平抛运动，根据平抛运动的规律，由牛顿第二定律和运动学公式结合进行分析．
解答：解：粒子在电场中做类平抛运动，平行于极板方向做匀速直线运动，垂直于极板方向做初速度为零的匀加速直线运动，则
运动时间为t=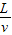
离开电场时垂直于极板方向的分速度为vy=at，加速度a=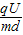
设偏转角度为θ，则tanθ=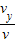
联立解得，tanθ=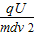
离开电场时的动能为Ek=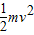
=
=
．
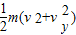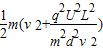由题，L、v、m、q、U均已知，故可求出θ、离开电场时的动能Ek、在电场中的运动时间t三个量．故ABD正确．
C、电势能是相对的，由于零电势点未知，无法求出离开电场时的电势能．故C错误．
故选ABD
点评：微粒在电场中做类平抛运动，运用运动的合成与分解处理类平抛运动问题是解决本题的关键．
解答：解：粒子在电场中做类平抛运动，平行于极板方向做匀速直线运动，垂直于极板方向做初速度为零的匀加速直线运动，则
运动时间为t=
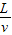
离开电场时垂直于极板方向的分速度为vy=at，加速度a=
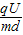
设偏转角度为θ，则tanθ=
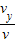
联立解得，tanθ=
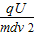
离开电场时的动能为Ek=
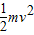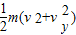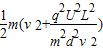==．由题，L、v、m、q、U均已知，故可求出θ、离开电场时的动能Ek、在电场中的运动时间t三个量．故ABD正确．
C、电势能是相对的，由于零电势点未知，无法求出离开电场时的电势能．故C错误．
故选ABD
点评：微粒在电场中做类平抛运动，运用运动的合成与分解处理类平抛运动问题是解决本题的关键．
练习册系列答案
相关题目
如图所示，能发射电子的阴极k和金属板P之间所加电压为U1，其右侧有一平行板电容器，已知平行板的板长为L，板间距离为d，且电容器的上极板带负电荷，下极板带等量的正电荷，在两极板间还存在有垂直于纸面的匀强磁场．从阴极k发出的电子被kP之间的电场加速后从P板上的小孔О射出，然后射入电容器并刚好从两板正中间沿直线ОО′射出电容器，如果在电子进入电容器前撤去板间电场而不改变磁场，则电子刚好能从平行板的右侧边缘射出，不计电子初速度、重力和电子间的相互作用，且整个装置放在真空中．求：
电子被kP之间的电场加速后从P板上的小孔О射出，然后射入电容器并刚好从两板正中间沿直线ОО′射出电容器，如果在电子进入电容器前撤去板间电场而不改变磁场，则电子刚好能从平行板
的右侧边缘射出，不计电子初速度、重力和电子间的相互作用，且整个装置放在真空中。求：
