Question

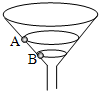如图所示：一轴竖直的锥形漏斗，内壁光滑，内壁上有两个质量相同的小球A、B各自在不同的水平面内做匀速圆周运动，则下列关系正确的有（　　）

A．线速度v_A＞v_B

B．角速度w_A＜w_B

C．向心加速度a_A＞a_B

D．小球对漏斗的压力N_A＞N_B

Answer 1

分析：小球做匀速圆周运动，因此合外力提供向心力，对物体正确进行受力分析，然后根据向心力公式列方程求解即可．

解答：解：A、设漏斗内壁母线与水平方向的夹角为θ．以任意一个小球为研究对象，分析受力情况：重力mg和漏斗内壁的支持力N，它们的合力提供向心力，如图，

则根据牛顿第二定律得
mgtanθ=m

v2

r

，得到v=

grtanθ

，θ一定，则v与

r

成正比，A球的圆周运动半径大于B球的圆周运动，所以v_A＞v_B，故A正确；．
B、角速度ω=

v

r

=

g r tanθ

，则角速度ω与

r

成反比，A球的圆周运动半径大于B球的圆周运动，所以角速度ω_A＜ω_B，故B正确；
C、向心加速度a=

v2

r

=gtanθ，与半径r和质量m无关，故a_A=a_B，故C错误；
D、漏斗内壁的支持力N=

mg

cosθ

，m，θ相同，则N_A=N_B，故D错误；
故选AB．

点评：解决这类圆周运动问题的关键是对物体正确受力分析，根据向心力公式列方程进行讨论，注意各种向心加速度表达式的应用．