题目内容
1.假设在赤道平面内有一颗侦察卫星绕地球做匀速圆周,某一时刻恰好处在另一颗同步卫星的正下方,已知侦察卫星的轨道半径为同步卫星的四分之一,则有( )| A. | 同步卫星和侦察卫星的线速度之比为2:1 | |
| B. | 同步卫星的和侦察卫星的角速度之比为8:1 | |
| C. | 再经过$\frac{12}{7}$h两颗卫星距离最远 | |
| D. | 再经过$\frac{6}{7}$h两颗卫星距离最远 |
分析 根据万有引力提供向心力公式,得到线速度、角速度与轨道半径的关系,在根据轨道半径的大小,求解线速度、角速度的关系,当两颗卫星的夹角为π时,相距最远,据此求解经过的时间.
解答 解:A、根据万有引力提供向心力$G\frac{Mm}{{r}^{2}}=m\frac{{v}^{2}}{r}$得:v=$\sqrt{\frac{GM}{r}}$,已知侦察卫星的轨道半径为同步卫星的四分之一,则同步卫星和侦察卫星的线速度之比为1:2,故A错误;
B、根据万有引力提供向心力$G\frac{Mm}{{r}^{2}}=m{ω}^{2}r$得:$ω=\sqrt{\frac{GM}{{r}^{3}}}$,则同步卫星的和侦察卫星的角速度之比为1:8,故B错误;
C、根据T=$\frac{2π}{ω}$可知,同步卫星的周期为24h,则角速度为${ω}_{1}=\frac{π}{12}$rad/s,则侦察卫星的角速度为${ω}_{2}=\frac{2π}{3}$rad/s
当两颗卫星的夹角为π时,相距最远,则有:t=$\frac{π}{{ω}_{2}-{ω}_{1}}=\frac{π}{\frac{7}{12}π}=\frac{12}{7}h$,故C正确,D错误.
故选:C
点评 本题关键是要掌握万有引力提供向心力这个关系,要求能够根据题意选择恰当的向心力的表达式.

练习册系列答案
相关题目
11.消防队员手持水枪灭火,水枪跟水平面有一仰角.关于水枪射出水流的射高和射程下落说法中正确的是( )
| A. | 初速度大小相同时,仰角越大,射程也越大 | |
| B. | 初速度大小相同时,仰角越大,射高也越高 | |
| C. | 仰角相同时,初速度越大,射高越大,射程不一定大 | |
| D. | 仰角相同时,初速度越大,射高越大,射程也一定大 |
12. 如图所示,光滑绝缘的半圆轨道竖直放置,直径AD水平,B、C是三等分点,在A、D两点固定有电荷量为Q1和Q2的正点电荷,电量满足关系:Q1=3$\sqrt{3}$Q2,且规定无穷远处电势为0,孤立正点电荷Q周围空间各点的电势为φ=k$\frac{Q}{r}$,Q表示电量,k表示静电力常量,r表示某点到点电荷的距离.则下列说法正确的是( )
如图所示,光滑绝缘的半圆轨道竖直放置,直径AD水平,B、C是三等分点,在A、D两点固定有电荷量为Q1和Q2的正点电荷,电量满足关系:Q1=3$\sqrt{3}$Q2,且规定无穷远处电势为0,孤立正点电荷Q周围空间各点的电势为φ=k$\frac{Q}{r}$,Q表示电量,k表示静电力常量,r表示某点到点电荷的距离.则下列说法正确的是( )
 如图所示,光滑绝缘的半圆轨道竖直放置,直径AD水平,B、C是三等分点,在A、D两点固定有电荷量为Q1和Q2的正点电荷,电量满足关系:Q1=3$\sqrt{3}$Q2,且规定无穷远处电势为0,孤立正点电荷Q周围空间各点的电势为φ=k$\frac{Q}{r}$,Q表示电量,k表示静电力常量,r表示某点到点电荷的距离.则下列说法正确的是( )
如图所示,光滑绝缘的半圆轨道竖直放置,直径AD水平,B、C是三等分点,在A、D两点固定有电荷量为Q1和Q2的正点电荷,电量满足关系:Q1=3$\sqrt{3}$Q2,且规定无穷远处电势为0,孤立正点电荷Q周围空间各点的电势为φ=k$\frac{Q}{r}$,Q表示电量,k表示静电力常量,r表示某点到点电荷的距离.则下列说法正确的是( )| A. | B点与C点的场强大小之比为EB:EC=$\sqrt{61}$:6 | |
| B. | B点与C点的场强大小之比为EB:EC=2$\sqrt{61}$:3 | |
| C. | B点与C点的电势大小之比为φB:φC=5$\sqrt{3}$:6 | |
| D. | B点与C点的电势大小之比为φB:φC=5$\sqrt{3}$:3 |
9.如图1是演示简谐运动图象的装置,当盛沙漏斗下面的薄木板N被匀速地拉出时,摆动着的漏斗中漏出的沙在板上形成的曲线显示出摆的位移随时间变化的关系,板上直线OO′代表时间轴.图2是一次实验中用同一个摆长不变的摆做出的两组操作形成的曲线,若板N1和N2拉动速度用v1和v2表示,板N1和N2上曲线所代表的摆动周期用T1和T2表示,则( )
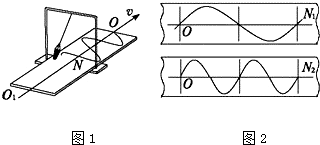

| A. | T1=2T2 | B. | 2T1=T2 | C. | v1=2v2 | D. | 2v1=v2 |
16.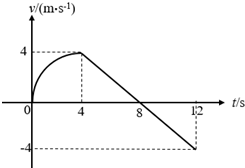 某质点在0~12s内运动的v-t图象如图所示.其中前4s内的图象是一段$\frac{1}{4}$圆弧,关于质点的运动,下列说法正确的是( )
某质点在0~12s内运动的v-t图象如图所示.其中前4s内的图象是一段$\frac{1}{4}$圆弧,关于质点的运动,下列说法正确的是( )
 某质点在0~12s内运动的v-t图象如图所示.其中前4s内的图象是一段$\frac{1}{4}$圆弧,关于质点的运动,下列说法正确的是( )
某质点在0~12s内运动的v-t图象如图所示.其中前4s内的图象是一段$\frac{1}{4}$圆弧,关于质点的运动,下列说法正确的是( )| A. | 质点在第一个4 s内的平均速度和在第二个4 s内的平均速度大小相等 | |
| B. | t=12 s时,质点的位移最大 | |
| C. | 质点在t=6 s时的加速度与t=10 s时的加速度大小相等,方向相反 | |
| D. | 质点在这12 s内的平均速度约为3 m/s |
6.如图1所示为一足够长的光滑斜面,一定质量的滑块从斜面的底端由静止开始在一沿斜面向上的外力作用下运动,经10s的时间撤走外力,利用速度传感器在计算机上描绘了滑块在0~30s内的速度-时间图象,如图2所示.则下列说法正确的是( )


| A. | 滑块在0~10 s内的平均速度等于10~20 s内的平均速度 | |
| B. | 滑块在0~30 s内的位移最大 | |
| C. | 滑块在10~20 s内的加速度与20~30 s内的加速度等大反向 | |
| D. | 滑块在10~20 s内的位移与20~30 s内的位移等大反向 |
13. 如图所示,天文学家观测到某行星和地球在同一轨道平面内绕太阳做同向匀速圆周运动,且行星的轨道半径比地球的轨道半径小,地球和太阳中心的连线与地球和行星的连线所夹的角叫做地球对该行星的观察视角(简称视角).已知该行星的最大视角为θ,当行星处于最大视角处时,是地球上的天文爱好者观察该行星的最佳时期.则地球绕太阳转动的角速度与行星绕太阳转动的角速度之比值为( )
如图所示,天文学家观测到某行星和地球在同一轨道平面内绕太阳做同向匀速圆周运动,且行星的轨道半径比地球的轨道半径小,地球和太阳中心的连线与地球和行星的连线所夹的角叫做地球对该行星的观察视角(简称视角).已知该行星的最大视角为θ,当行星处于最大视角处时,是地球上的天文爱好者观察该行星的最佳时期.则地球绕太阳转动的角速度与行星绕太阳转动的角速度之比值为( )
 如图所示,天文学家观测到某行星和地球在同一轨道平面内绕太阳做同向匀速圆周运动,且行星的轨道半径比地球的轨道半径小,地球和太阳中心的连线与地球和行星的连线所夹的角叫做地球对该行星的观察视角(简称视角).已知该行星的最大视角为θ,当行星处于最大视角处时,是地球上的天文爱好者观察该行星的最佳时期.则地球绕太阳转动的角速度与行星绕太阳转动的角速度之比值为( )
如图所示,天文学家观测到某行星和地球在同一轨道平面内绕太阳做同向匀速圆周运动,且行星的轨道半径比地球的轨道半径小,地球和太阳中心的连线与地球和行星的连线所夹的角叫做地球对该行星的观察视角(简称视角).已知该行星的最大视角为θ,当行星处于最大视角处时,是地球上的天文爱好者观察该行星的最佳时期.则地球绕太阳转动的角速度与行星绕太阳转动的角速度之比值为( )| A. | $\sqrt{{{tan}^3}θ}$ | B. | $\sqrt{{{sin}^3}θ}$ | C. | $\sqrt{\frac{1}{{{{sin}^3}θ}}}$ | D. | $\sqrt{\frac{1}{{{{tan}^3}θ}}}$ |
10.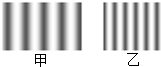 图甲、图乙为两次用单色光做双缝干涉实验时,屏幕上显示的图样.图甲条纹间距明显大于图乙,比较两次实验( )
图甲、图乙为两次用单色光做双缝干涉实验时,屏幕上显示的图样.图甲条纹间距明显大于图乙,比较两次实验( )
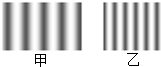 图甲、图乙为两次用单色光做双缝干涉实验时,屏幕上显示的图样.图甲条纹间距明显大于图乙,比较两次实验( )
图甲、图乙为两次用单色光做双缝干涉实验时,屏幕上显示的图样.图甲条纹间距明显大于图乙,比较两次实验( )| A. | 若光屏到双缝的距离相等,则图甲对应的波长较大 | |
| B. | 若光源、双缝间隙相同,则图甲光屏到双缝的距离较大 | |
| C. | 若光源、光屏到双缝的距离相同,则图甲双缝间隙较小 | |
| D. | 图甲的光更容易产生明显的衍射现象 |
10.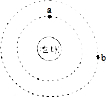 如图,若两颗人造卫星a和b均绕地球作匀速圆周运动,且a、b在运动过程中仅受地球万有引力的作用,a、b绕地球运动的线速度大小分别为v1、v2,周期分别为T1、T2,则( )
如图,若两颗人造卫星a和b均绕地球作匀速圆周运动,且a、b在运动过程中仅受地球万有引力的作用,a、b绕地球运动的线速度大小分别为v1、v2,周期分别为T1、T2,则( )
 如图,若两颗人造卫星a和b均绕地球作匀速圆周运动,且a、b在运动过程中仅受地球万有引力的作用,a、b绕地球运动的线速度大小分别为v1、v2,周期分别为T1、T2,则( )
如图,若两颗人造卫星a和b均绕地球作匀速圆周运动,且a、b在运动过程中仅受地球万有引力的作用,a、b绕地球运动的线速度大小分别为v1、v2,周期分别为T1、T2,则( )| A. | lg($\frac{{v}_{1}}{{v}_{2}}$)=$\frac{1}{3}$lg($\frac{{T}_{1}}{{T}_{2}}$) | B. | lg($\frac{{v}_{1}}{{v}_{2}}$)=3lg($\frac{{T}_{1}}{{T}_{2}}$) | ||
| C. | lg($\frac{{v}_{1}}{{v}_{2}}$)=$\frac{1}{3}$lg($\frac{{T}_{2}}{{T}_{1}}$) | D. | lg($\frac{{v}_{1}}{{v}_{2}}$)=3lg($\frac{{T}_{2}}{{T}_{1}}$) |