题目内容
如图，一小物块初速v1，开始由A点沿水平面滑至B点时速度为v2，若该物块仍以速度v1从A点沿两斜面滑动至B点时速度为v2′，已知斜面和水平面与物块的动摩擦因数相同，则（ ）分析：物体从A点滑动到B过程中，根据动能定理列式，该物块仍以速度v1从A点沿两斜面滑动至B点的过程中，设最高点为C点，AC与水平面的夹角为θ，CB与水平面的夹角为α，根据动能定理列式，比较两个方程即可求解．
解答：解：物体从A点滑动到B过程中，根据动能定理有：
mv22-
mv12=μmgxAB ①
若该物块仍以速度v1从A点沿两斜面滑动至B点的过程中，设最高点为C点，AC与水平面的夹角为θ，CB与水平面的夹角为α，则有：
mv′22-
mv12=μmgcosθ?xAC+μmgcosα?xBC=μmgxAB ②
由①②解得：v2=v2′
由A点沿水平面滑至B点做匀减速运动，而沿两斜面运动时，先匀减速后匀加速，到达B点时速度相同，所以沿斜面运动的速度都比沿直线运动时的速度小，所以时间比沿直线运动的时间长，故D错误．
故选：C
| 1 |
| 2 |
| 1 |
| 2 |
若该物块仍以速度v1从A点沿两斜面滑动至B点的过程中，设最高点为C点，AC与水平面的夹角为θ，CB与水平面的夹角为α，则有：
| 1 |
| 2 |
| 1 |
| 2 |
由①②解得：v2=v2′
由A点沿水平面滑至B点做匀减速运动，而沿两斜面运动时，先匀减速后匀加速，到达B点时速度相同，所以沿斜面运动的速度都比沿直线运动时的速度小，所以时间比沿直线运动的时间长，故D错误．
故选：C
点评：本题关键根据动能定理列式，对列得的方程进行讨论得出结论．
练习册系列答案
相关题目
如图所示，平板小车沿水平地面始终以加速度a做匀加速直线运动．当小车速度增至v时，将一小物块无初速地放于平板小车的A端（小车的加速度保持不变）．物块与小车间的动摩擦因数为μ，（μg＞a），要使物块不会从小车上滑出，求平板小车的最小长度L0．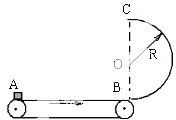
如图所示，一水平传送带始终保持着大小为v=4m/s的速度做匀速运动．在传送带右侧有一半圆弧形的竖直放置的光滑圆弧轨道，其半径为R=0.2m，半圆弧形轨道最低点与传送带右端B衔接并相切，一小物块无初速地放到皮带左端A处，经传送带和竖直圆弧轨道至最高点C．已知当A、B之间距离为s=1m时，物块至最高点对轨道的压力为零，（g=10m/s2）则：
应满足什么条件？
应满足什么条件？
