Question

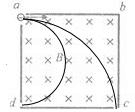
如图所示为一正方形空腔的横截面，a、b、c为三个小孔（孔径不计），腔内有一垂直于纸面向里的匀强磁场，一束具有不同速率的电子，由孔a垂直磁场方向射入空腔．如从孔b、c分别有电子射出，则从两孔射出电子的速率之比V_b：V_c=

1：2

，飞行时间之t_b：t_c=

2：1

．

Answer 1

分析：带电粒子在磁场中做圆周运动，由几何知识可分别求得从c点和d点飞出的粒子的半径，则由向心力公式可求得各自的速率及比值；由转动的角度可知运动时间之比．

解答：解：设磁场边长为a，如图所示，粒子从c点离开，其半径为a；

由BqV_c=m

v 2 c

a

可得：
vc=

eBa

m

；
粒子从b点离开，其半径为

a

2

；
则vb=

eBa

2m

故

vb

vc

=

1

2

；
粒子的运行周期T=

2πr

v

=

2πm

eB

，与速度无关；
从c点离开的粒子运行的时间t_c=

T

4

从d点离开的粒子运行的时间t_b=

T

2

；
故

tb

tc

=

2

1

；
故答案为：1：2；  2：1．

点评：本题属于带电粒子在磁场中的偏转中典型题目，此类题的关键在于确定圆心及由几何关系求出半径．