题目内容
如图所示的正方形abcd空腔内磁场均匀．一束速率不同的电子沿平行ab的方向垂直打入匀强磁场．一些电子从孔c穿出，另一些电子从孔d穿出，这两部分电子的速率v、周期T及在磁场中运动的时间t、动能Ek之间的关系为（ ）| A、vc：vd=2：1 | B、Tc：Td=2：1 | C、tc：td=1：2 | D、Ekc：Ekd=1：2 |
分析：带电粒子在磁场中做圆周运动，由几何知识可分别求得从c点和d点飞出的粒子的半径，则由向心力公式可求得各自的速率及比值；由转动的角度可知运动时间之比．
解答：解：设磁场边长为a，如图所示，粒子从c点离开，其半径为a；
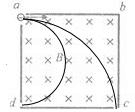
A、B：由洛伦兹力提供向心力得：Bqvc=
可得：vc=
；
粒子从d点离开，其半径为
；
同理可得：vd=
，故vc：vd=2：1．故A正确，B错误；
C、粒子的运行周期：T=
，因此它们的周期之比1：1；
从图可得，从c点离开的粒子运行的时间是
个周期：tc=
从d点离开的粒子运行的时间是半个周期：td=
；
故tc：td=1：2； 故C正确，
D、由A选项分析可知，它们的动能之比与速率的平方成正比，所以Ekc：Ekd=4：1；故D错误．
故选：AC．
A、B：由洛伦兹力提供向心力得：Bqvc=
m
| ||
| a |
| Bqa |
| m |
粒子从d点离开，其半径为
| a |
| 2 |
同理可得：vd=
| Bqa |
| 2m |
C、粒子的运行周期：T=
| 2πm |
| qB |
从图可得，从c点离开的粒子运行的时间是
| 1 |
| 4 |
| T |
| 4 |
从d点离开的粒子运行的时间是半个周期：td=
| T |
| 2 |
故tc：td=1：2； 故C正确，
D、由A选项分析可知，它们的动能之比与速率的平方成正比，所以Ekc：Ekd=4：1；故D错误．
故选：AC．
点评：本题属于带电粒子在磁场中的偏转中典型题目，此类题的关键在于确定圆心及由几何关系求出半径．
练习册系列答案
相关题目
如图所示的正方形abcd内有垂直于纸面向里的匀强磁场，两个带电粒子P、Q以相同的初速度从a点沿ab方向射入该区域后，分别从d、c点射出（不考虑粒子重力和粒子间的相互作用），粒子运动轨迹如图所示．下列说法中正确的是（ ）| A、P、Q带的是正电荷 | B、P、Q两粒子的荷质比为1：2 | C、P、Q两粒子在磁场中经历的时间相同 | D、P、Q两粒子在磁场中的加速度大小之比为1：2 |
